Then
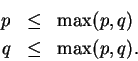
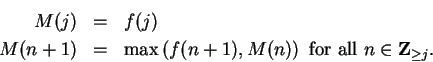
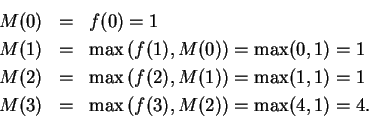
Proof: Let ![]() be the proposition form on
be the proposition form on
![]() such that
such that ![]() is the
proposition (3.92). Then
is the
proposition (3.92). Then ![]() says
says
Now for all
![]() ,
,
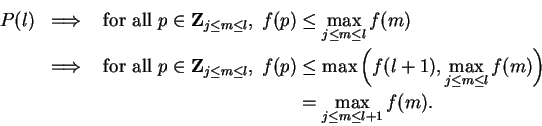
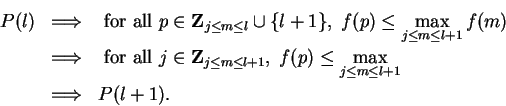
a^n.
The notation ![]() for the factorial of
for the factorial of ![]() was introduced by
Christian Kramp
in 1808[15, vol 2, p 66].
was introduced by
Christian Kramp
in 1808[15, vol 2, p 66].
The use of the Greek letter ![]() to denote sums was introduced
by Euler
in 1755[15, vol 2,p 61].
Euler writes
to denote sums was introduced
by Euler
in 1755[15, vol 2,p 61].
Euler writes
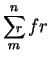 to denote
what we would write
as
to denote
what we would write
as
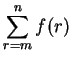 [15, vol 2, p 61].
[15, vol 2, p 61].
In Maple,
the value of
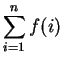 is denoted
by
is denoted
by sum(f(i),i=1..n)![]() . In Mathematica
it
is denoted by
. In Mathematica
it
is denoted by Sum[f[i],{i,1,n}]![]() .
.