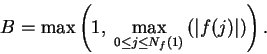Next: 7.6 Geometric Series
Up: 7. Complex Sequences
Previous: 7.4 Sums and Products
Index
Proof: By definition 7.10, `` 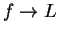 " means
" means
for every
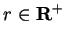
there
is some
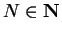
such that
for every
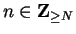
,
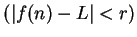
.
By definition 7.11, `` 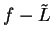 is a null sequence" means
is a null sequence" means
Both definitions say the same thing. If we write out the definition for ``
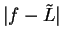 is a null sequence" we get (7.30) with ``
is a null sequence" we get (7.30) with ``
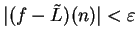 " replaced by
" replaced by
``
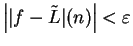 ." Since
." Since
conditions b) and c) are equivalent.

Proof:
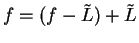 .
.

Proof: Suppose 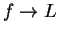 and
and 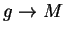 .
By the decomposition theorem, we can write
.
By the decomposition theorem, we can write
where 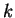 and
and 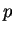 are null sequences. Then
are null sequences. Then
By the sum theorem for null sequences, 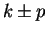 is a null sequence, so
is a null sequence, so
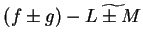 is a null sequence, and hence
is a null sequence, and hence
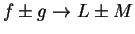 .
.

7.33
Exercise.
Prove the last statement in theorem
7.32; i.e., show that if
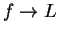
then
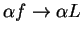
for all
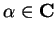
.
7.34
Theorem (Product theorem for convergent sequences.)
Let  be convergent complex sequences. Suppose
be convergent complex sequences. Suppose 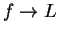 and
and 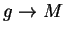 . Then
. Then 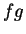 is
convergent and
is
convergent and 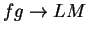 .
.
Proof: Suppose 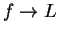 and
and 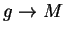 . Write
. Write 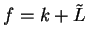 ,
, 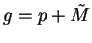 where
where
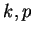 are null sequences. Then
are null sequences. Then
Now 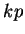 ,
, 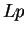 and
and 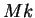 are null sequences by the product theorem and sum theorem for
null sequences, and
are null sequences by the product theorem and sum theorem for
null sequences, and
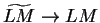 , so by several applications of the sum
theorem for convergent sequences,
, so by several applications of the sum
theorem for convergent sequences,
7.35
Theorem (Uniqueness theorem for convergent sequences.)
Let
 be a complex sequence, and let
be a complex sequence, and let
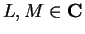 . If
. If 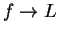 and
and 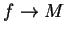 , then
, then
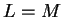 .
.
Proof: Suppose 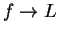 and
and 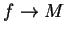 . Then
. Then 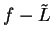 and
and 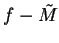 are null
sequences, so
are null
sequences, so
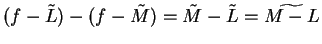 is a null
sequence. Hence, by theorem 7.15,
is a null
sequence. Hence, by theorem 7.15, 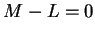 ; i.e.,
; i.e., 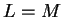 .
.

7.36
Definition (Limit of a sequence.)
Let

be a convergent sequence. Then the unique complex number
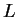
such that
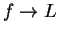
is denoted by
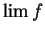
or
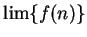
.
7.37
Remark.
It follows from the sum and product theorems that if

and

are convergent
sequences, then
and
and
7.38
Warning.
We have only defined
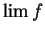
when

is a convergent sequence. Hence
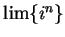
is ungrammatical and should not be written down. (We showed in theorem
7.7 that
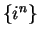
diverges.) However, it is a standard
usage to say ``
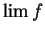
does not exist'' or ``
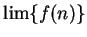
does
not exist'' to mean that the sequence

has no limit. Hence we may say ``
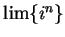
does not exist''.
Proof: If
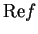 and
and
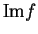 are convergent, then it follows from the sum
theorem for convergent sequences that
are convergent, then it follows from the sum
theorem for convergent sequences that  is convergent and (7.40) is valid.
is convergent and (7.40) is valid.
Suppose that 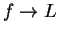 . Then
. Then 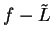 is a null sequence, so
is a null sequence, so
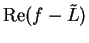 is a null sequence (by Theorem 7.26). For all
is a null sequence (by Theorem 7.26). For all
 ,
,
so
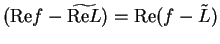 is a null sequence and it
follows that
is a null sequence and it
follows that
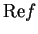 converges to
converges to
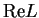 . A similar argument shows that
. A similar argument shows that
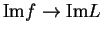 .
.

7.41
Definition (Bounded sequence.)
A sequence

in

is
bounded, if there is a disc
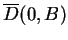
such that
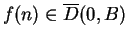
for all

; i.e.,

is bounded if there is a number
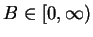
such that
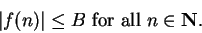 |
(7.42) |
Any number
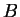
satisfying condition (
7.42) is called a
bound for 
.
7.43
Examples.
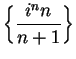
is bounded since
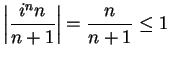
for all

. The
sequence
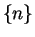
is not bounded since the statement
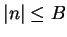
for all

contradicts the Archimedean property of

. Every constant sequence
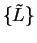
is bounded. In fact,
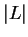
is a bound for
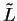
.
7.44
Exercise (Null-times-bounded theorem.)
A
Show that if

is a null sequence in

, and

is a bounded sequence in

then
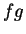
is
a null sequence.
The next theorem I want to prove is a quotient theorem for convergent sequences. To
prove this, I will need some technical results.
7.45
Theorem (Reverse triangle inequality.)
Let
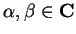 , then
, then
Proof: By the triangle inequality.
Hence,
7.46
Lemma.
Let  be a convergent sequence
that is not a null sequence; i.e.,
be a convergent sequence
that is not a null sequence; i.e.,
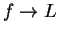 where
where 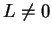 . Suppose
. Suppose 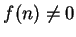 for all
for all
 . Then
. Then
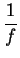 is a bounded sequence.
is a bounded sequence.
Proof: Since 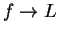 , we know that
, we know that 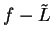 is a null sequence. Let
is a null sequence. Let
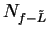 be a
precision function for
be a
precision function for 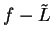 . Then for all
. Then for all
 ,
,
i.e., if
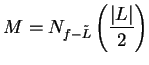 , then
, then
Let
Then
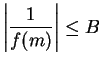 for
for
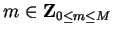 and
and
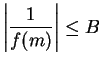 for
for
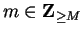 , so
, so
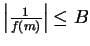 for all
for all
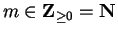 , and hence
, and hence
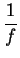 is bounded.
is bounded.

7.47
Theorem (Reciprocal theorem for convergent sequences.)
Let  be a complex sequence. Suppose that
be a complex sequence. Suppose that 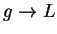 where
where 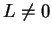 , and that
, and that
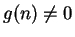 for all
for all
 . Then
. Then
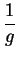 is convergent, and
is convergent, and
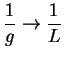 .
.
Proof: By the preceding lemma,
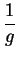 is a bounded sequence, and since
is a bounded sequence, and since
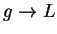 , we know that
, we know that 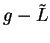 is a null sequence. Hence
is a null sequence. Hence
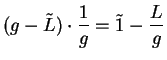 is a null sequence, and it follows that
is a null sequence, and it follows that
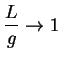 . Then we have
. Then we have
i.e.,
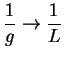 .
.

7.49
Exercise.
A
- a)
- Let
 be complex sequences.
Show that if
be complex sequences.
Show that if  converges
and
converges
and  diverges, then
diverges, then 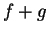 diverges.
diverges.
- b)
- Show that if
 converges and
converges and  diverges, then
diverges, then 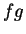 does not necessarily
diverge.
does not necessarily
diverge.
7.50
Exercise.
A
Let

be a divergent complex sequence.
Show that if
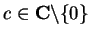
, then
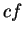
is divergent.
7.51
Example.
Let
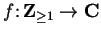
be defined by
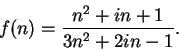 |
(7.52) |
Then
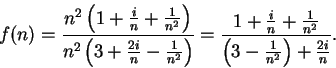 |
(7.53) |
Hence

can be written as a quotient of two sequences:
and
where
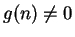
for all
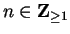
.
Since
and
it
follows from numerous applications of product and sum rules that
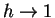
and
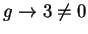
and hence
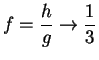
. Once I have expressed
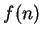
in
the final form in (
7.53), I can see what the final result is, and I will usually
just write
7.54
Example.
Let
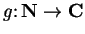
be the sequence
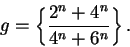 |
(7.55) |
Then for all

,
Since
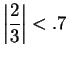
, I know
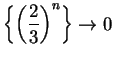
and
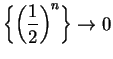
so
In the last two examples, I was motivated by the following considerations. I think:
In the numerator and denominator for (7.52), for large 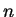 the ``
the `` 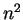 "
term overwhelms the other terms - so that's the term I factored out. In the
numerator of (7.55), the overwhelming term is
"
term overwhelms the other terms - so that's the term I factored out. In the
numerator of (7.55), the overwhelming term is 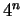 , and in the denominator,
the overwhelming term is
, and in the denominator,
the overwhelming term is 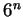 so those are the terms I factored out.
so those are the terms I factored out.
7.56
Exercise.
A
Let
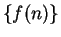
be a sequence of non-negative numbers
and suppose
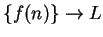
where
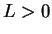
. Prove that
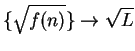
. (NOTE:
The case
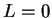
follows from the root theorem for null sequences.
7.58
Exercise.
A
Show that the sum of two
bounded sequences is a bounded
sequence.
7.59
Theorem (Convergent sequences are bounded.)
Let 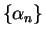 be a convergent complex sequence. Then
be a convergent complex sequence. Then
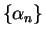 is bounded.
is bounded.
Proof: I will show that null sequences are bounded and leave the general case to
you. Let  be a null sequence and let
be a null sequence and let 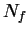 be a precision function for
be a precision function for  .
.
Let
I claim that 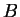 is a bound for
is a bound for  . If
. If
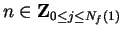 , then
, then
If
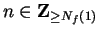 , then
, then 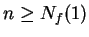 , so
, so
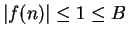 . Hence
. Hence
i.e., 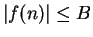 for all
for all
 .
.

7.60
Exercise.
A
Complete the proof of theorem
7.59; i.e., show that if
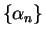
is a convergent complex sequence, then
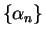
is bounded.
7.61
Example.
It follows from the fact that convergent sequences are bounded, that
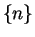
is not a convergent sequence.
7.62
Exercise.
Give an example of a bounded sequence that is not convergent.




Next: 7.6 Geometric Series
Up: 7. Complex Sequences
Previous: 7.4 Sums and Products
Index
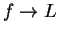
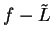 is a null sequence.
is a null sequence.
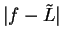 is a null sequence.
is a null sequence.
![]() " means
" means
![]() is a null sequence" means
is a null sequence" means
![]() .
.
![]()
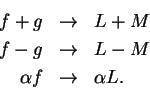
![]() and
and ![]() .
By the decomposition theorem, we can write
.
By the decomposition theorem, we can write
![]() and
and ![]() . Write
. Write ![]() ,
, ![]() where
where
![]() are null sequences. Then
are null sequences. Then
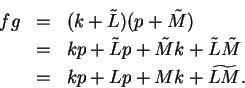
![]() and
and ![]() . Then
. Then ![]() and
and ![]() are null
sequences, so
are null
sequences, so
![]() is a null
sequence. Hence, by theorem 7.15,
is a null
sequence. Hence, by theorem 7.15, ![]() ; i.e.,
; i.e., ![]() .
.
![]()
![]() and
and
![]() are convergent, then it follows from the sum
theorem for convergent sequences that
are convergent, then it follows from the sum
theorem for convergent sequences that ![]() is convergent and (7.40) is valid.
is convergent and (7.40) is valid.
![]() . Then
. Then ![]() is a null sequence, so
is a null sequence, so
![]() is a null sequence (by Theorem 7.26). For all
is a null sequence (by Theorem 7.26). For all
![]() ,
,
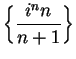 is bounded since
is bounded since
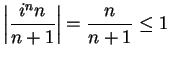 for all
for all
![]() , we know that
, we know that ![]() is a null sequence. Let
is a null sequence. Let
![]() be a
precision function for
be a
precision function for ![]() . Then for all
. Then for all
![]() ,
,
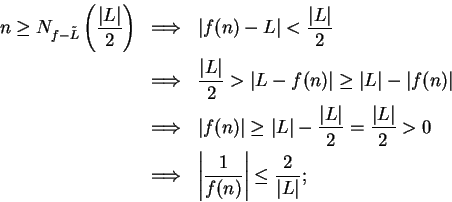
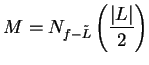 , then
, then
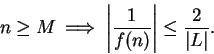
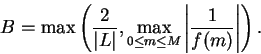
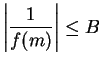 for
for
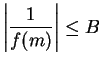 for
for
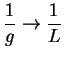 .
.
![]() is a bounded sequence, and since
is a bounded sequence, and since
![]() , we know that
, we know that ![]() is a null sequence. Hence
is a null sequence. Hence
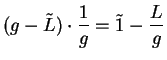 is a null sequence, and it follows that
is a null sequence, and it follows that
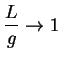 . Then we have
. Then we have
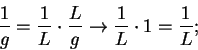
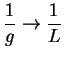 .
.
![]() be convergent complex sequences. If
be convergent complex sequences. If ![]() and
and ![]() , then
, then
![]() is convergent and
is convergent and
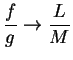 .
.
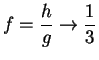 . Once I have expressed
. Once I have expressed 
![]() the ``
the `` ![]() "
term overwhelms the other terms - so that's the term I factored out. In the
numerator of (7.55), the overwhelming term is
"
term overwhelms the other terms - so that's the term I factored out. In the
numerator of (7.55), the overwhelming term is ![]() , and in the denominator,
the overwhelming term is
, and in the denominator,
the overwhelming term is ![]() so those are the terms I factored out.
so those are the terms I factored out.
 . (NOTE:
The case
. (NOTE:
The case 
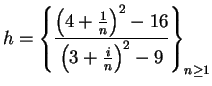
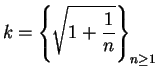
![]() be a null sequence and let
be a null sequence and let ![]() be a precision function for
be a precision function for ![]() .
.