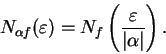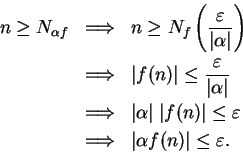


Next: 7.5 Theorems About Convergent
Up: 7. Complex Sequences
Previous: 7.3 Null Sequences
Index
7.4 Sums and Products of Null Sequences
7.27
Theorem (Sum theorem for null sequences.)Let 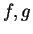 be complex null sequences and let
be complex null sequences and let
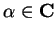 . Then
. Then 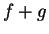 ,
, 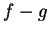 , and
, and 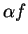 are null sequences.
are null sequences.
Scratchwork for 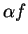 : I want to find
: I want to find 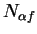 so
that
so
that
i.e.
This suggests that I
take
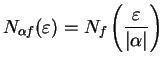 .
.
Scratchwork for 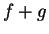 : I want to find
: I want to find 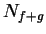 so that
so that
Now
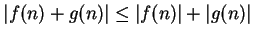 , and I can make
, and I can make
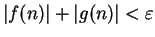 by making
by making
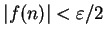 and
and
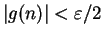 . Hence I want
. Hence I want
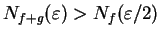 and
and
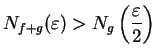 . This suggests that
I take
. This suggests that
I take
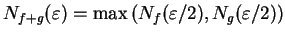 .
.
Proof: Let 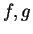 be null sequences, and let
be null sequences, and let
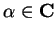 . Define
. Define
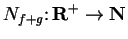 by
by
Then for all
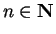 ,
,
Hence, 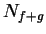 is a precision function for
is a precision function for 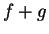 , and
, and 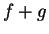 is a null sequence.
is a null sequence.
If 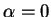 then
then
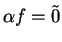 is a null sequence. Suppose
is a null sequence. Suppose 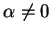 ,
and define
,
and define
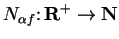 by
by
Then for all
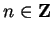 ,
,
Hence 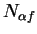 is a precision function for
is a precision function for 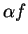 , and hence
, and hence 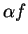 is
a null sequence.
Since
is
a null sequence.
Since 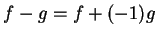 it follows that
it follows that 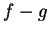 is a null sequence.
is a null sequence.
7.28
Exercise (Product theorem for null sequences.)
A
Let
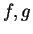
be complex null sequences.
Prove that
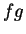
is a null
sequence.



Next: 7.5 Theorems About Convergent
Up: 7. Complex Sequences
Previous: 7.3 Null Sequences
Index
![]() : I want to find
: I want to find ![]() so
that
so
that
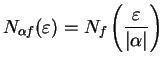 .
.
![]() : I want to find
: I want to find ![]() so that
so that
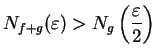 . This suggests that
I take
. This suggests that
I take
![]() be null sequences, and let
be null sequences, and let
![]() . Define
. Define
![]() by
by
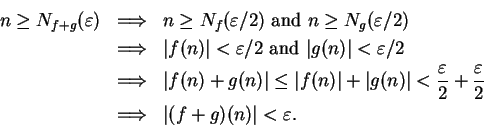
![]() then
then
![]() is a null sequence. Suppose
is a null sequence. Suppose ![]() ,
and define
,
and define
![]() by
by