1.3 Equality

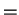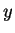
1.34   Notation ($=$.) Let $x$ and $y$ be (names of) objects. I write

$$x=y$$

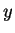
to mean that $x$ and $y$ are names for the same object. I will not make a distinction between an object and its name.

$$\mbox{ For all objects } x,\quad x = x. \index{reflexivity of equality}$$ (1.35)

We describe this property by saying that equality is reflexive.

$$\mbox{ For all objects } x,y, \quad (x=y)\mbox{$\hspace{1ex}\Longrightarrow\hspace{1ex}$}(y=x). \index{symmetry of equality}$$ (1.36)

We describe this property by saying that equality is symmetric.

$$\mbox{ For all objects } x,y,z \;\; \left((x=y) \mbox{ and }... ...\right)\mbox{$\hspace{1ex}\Longrightarrow\hspace{1ex}$} (x=z).$$ (1.37)

We describe this property by saying that equality is transitive.

Let $P$ be a proposition involving the object $x$. Let $Q$ be a proposition obtained by replacing any or all occurrences of $x$ in $P$ by $y$. Then $P\mbox{$\Longleftrightarrow$}Q$. We call this property of equality the substitution property.

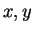
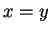
1.38   Examples. Suppose that $x,y$ are integers, and $x=y$. Then

$$\Big((x+3)(x+4)=28+x\Big)\hspace{1ex}\Longleftrightarrow\hspace{1ex}\Big((x+3)(y+4)=28+y\Big),$$

and

$$\Big((x+3)(x+4)=28+x\Big)\iff\Big((y+3)(y+4)=28+y\Big),$$

and

$$\Big((x+3)(x+4)=28+x\Big)\hspace{1ex}\Longleftrightarrow\hspace{1ex}\Big((y+3)(x+4)=28+x\Big).$$

We will frequently make statements like

$$(x=y)\mbox{$\hspace{1ex}\Longrightarrow\hspace{1ex}$}(x+3=y+3).$$

The justification for this is

$$x+3=x+3 \qquad \mbox{ (by reflexivity of } =.)$$

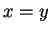
Hence, if $x=y$, then by the substitution property,

$$x+3=y+3.$$

1.39   Warning. Because we are using a vague notion of proposition, the substitution property of equality as stated is not precisely true. For example, although

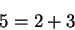$$5=2+3$$ (1.40)

and

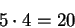$$5\cdot 4=20$$ (1.41)

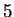
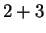
are both true, the result of substituting the $5$ in the second equation by $2+3$ yields

$$2+3\cdot 4=20$$

which is false.

The proper conclusion that follows from (1.40) and (1.41) is

$$(2+3)\cdot 4=20.$$

(The use of parentheses is discussed in Remark 2.50.)

1.42   Notation ($a=b=c=d.$) Let $a,b,c,d$ be objects. We write

$$a=b=c=d$$ (1.43)

as an abbreviation for

$$\left((a=b) \mbox{ and } (b=c)\right) \mbox{ and } (c=d).$$

If (1.43) is true, then by several applications of transitivity, we conclude that

$$a=d.$$