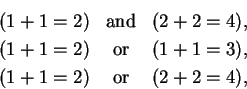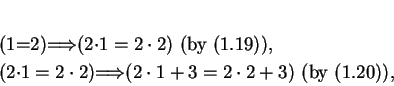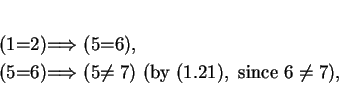Next: 1.3 Equality
Up: 1. Notation, Undefined Concepts
Previous: 1.1 Sets
Index
1.11
Definition (Proposition.)
A
proposition is a statement that is either true or false.
1.12
Examples.
Both
and
are propositions. The first is true and the second is false. I will consider
to be a proposition, because I expect that you know what a prime number is. However,
I will not consider
to be a proposition (unless I provide you with a definition for
unlucky number).
The proposition
is true, and the proposition
is false, but
is not a
proposition but rather a meaningless statement (cf (
1.8)).
Observe that ``
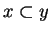
'' makes sense whenever

and
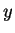
are sets,
and ``
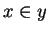
'' makes sense when
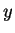
is a set, and

is any object.
Similarly
is meaningless rather than false, since division by zero is not defined., i.e.
I do not consider
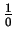
to be a name for any object.
1.13
Definition (and, or, not.)
If

and
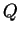
are propositions, then
are propositions, and (

or
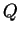
) is true if and only if at least one of
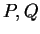
is
true; (

and
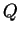
) is true if and only if both of
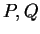
are true; (not

) is true
if and only if

is false.
1.14
Example.
are all true propositions.
1.15
Notation (
 .)
.)
We abbreviate
and we abbreviate
1.16
Notation (
 )
)
If

and
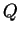
are propositions, we write
 |
(1.17) |
to denote the proposition ``

implies
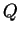
".
1.18
Example.
If
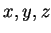
are integers then all of the following are true:
The three main properties of implication that we will use are:
We denote property (1.22) by saying that
 is transitive.
is transitive.
1.23
Example.
The meaning of a statement like
 |
(1.24) |
or
 |
(1.25) |
may not be obvious. I claim that both (
1.24) and (
1.25) should be true.
``Proof'' of (1.24):
and
so by transitivity of
,
``Proof'' of (1.25):
so
so
The previous example is supposed to motivate the following assumption:
A false proposition implies everything,
i.e.
If

is false, then
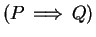
is true for all propositions
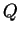
.
1.26
Example.
For every
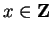
, the proposition
is true. Hence all three of the statements below are true:
Proposition (1.28) is an example of a false statement implying a true one, and
proposition (1.29) is an example of a false statement implying a false one.
Equations (1.27) and (1.28) together provide motivation for the
assumption.
Every statement implies a true statement;
i.e.
If
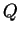
is true then
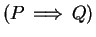
is true for all propositions

.
The following table shows the conditions under which
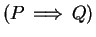 is true.
is true.
 |
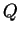 |
 |
| true |
true |
true |
| true |
false |
false |
| false |
true |
true |
| false |
false |
true |
Thus a true statement does not imply a false one. All other sorts of implications
are valid.
1.30
Notation (
 .)
.)
Let

,
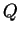
,
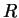
,

be propositions. Then
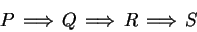 |
(1.31) |
is an abbreviation for
It follows from transitivity of
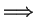
that if (
1.31) is true,
then
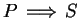
is true.
Note that (1.31) is not an abbreviation for
i.e., when I write (1.31), I do not assume that  is true.
is true.
1.32
Definition (Equivalence of propositions,
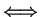 .)
.)
Let
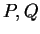
be propositions. We say that

and
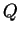
are
equivalent and write
(read this ``

is equivalent to
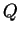
" or ``

if and only if
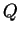
") to mean
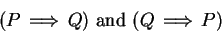 |
(1.33) |
If either (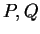 are both true) or (
are both true) or (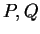 are both false), then
are both false), then
 is
true. If one of
is
true. If one of 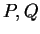 is false, and the other is true,
then one of
is false, and the other is true,
then one of
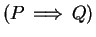 ,
,
 has the form
has the form 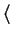 true
true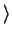
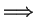
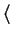 false
false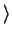 , and hence in this case
, and hence in this case
 is false. Thus
is false. Thus

is true if and only if
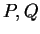
are both true or both false.




Next: 1.3 Equality
Up: 1. Notation, Undefined Concepts
Previous: 1.1 Sets
Index