



Next: 2.2 Some Examples
Up: 2. Fields
Previous: 2. Fields
Index
2.1
Definition (Binary operation.)
Let

be a set. A
binary operation on

is a function
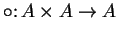
. Binary operations are usually denoted by special symbols such as
rather than by letters. If
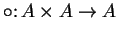
is a binary operation, we
write
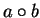
instead of
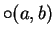
. By the definition of function
(
1.57), a binary operation is a triple
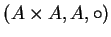
, but as is
usual for functions, we refer to `` the binary operation

" instead of
`` the binary operation
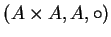
".
2.2
Examples.
The usual operations of addition
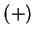
, subtraction
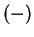
and multiplication
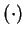
are binary operations on
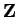
and on
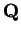
. Subtraction is not a binary
operation on
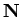
, because
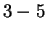
is not in
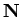
. Division is not a binary operation
on
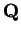
, because division by

is not defined. However, division is a binary
operation on
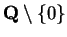
.
Let
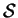 be the set of all sets.2.1 Then union
be the set of all sets.2.1 Then union 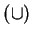 and intersection
and intersection 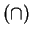 and set
difference
and set
difference 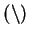 are binary operations on
are binary operations on
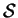 .
.
Let
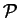 be the set of all propositions. Then and and or are binary
operations on
be the set of all propositions. Then and and or are binary
operations on
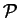 . In mathematical logic, and is usually represented by
. In mathematical logic, and is usually represented by 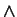 or
or 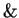 ,
and or is represented by
,
and or is represented by 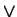 or
or 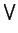 .
.
2.3
Definition (Identity element.)
Let

be a binary operation on a set

. An element
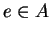
is an
identity element for 
(or just an
identity for 
) if
2.4
Examples.

is an identity for addition on
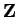
, and
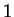
is an identity for
multiplication on
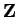
. There is no identity for subtraction on
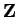
, since for
all
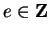
we have
Since (
2.5) is false, the first statement is also false; i.e., for all
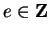
,
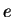
is not an identity for
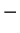
.

2.6
Exercise.
Let
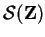
denote the set of all subsets of
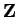
. Then
union
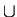
and intersection
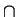
are binary operations on
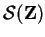
. Is there
an identity element for
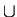
? If so, what is it? Is there an identity element for
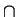
? If so, what is it?
2.7
Theorem (Uniqueness of identities.)
Let  be a binary operation on a set
be a binary operation on a set  . Suppose that
. Suppose that 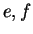 are both identity
elements for
are both identity
elements for  . Then
. Then 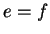 . (Hence we usually talk about the identity
for
. (Hence we usually talk about the identity
for  , rather than an identity for
, rather than an identity for  .)
.)
Proof: Let 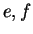 be identity elements for
be identity elements for  . Then
. Then
and
It follows that 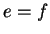 .
.

2.8
Remark.
The conclusion of the previous proof used transitivity of equality
1.37). I usually use the properties of equality without
explicitly mentioning them.
2.9
Definition (Inverse.)
Let

be a binary operation on a set

, and suppose that there is an identity
element
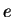
for

. (We know that this identity is unique.) Let

be an
element of

. We say that an element
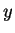
of
 is an inverse for
is an inverse for  under
under 
if
We say that

is
invertible under 
if

has an inverse under

.
2.11
Exercise.
A
Let
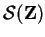
be the set of all subsets of
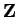
. In exercise
2.6
you should have shown that both of the operations
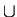
and
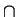
on
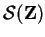
have identity elements.
- a
- Which subsets
 of
of
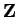 have inverses for
have inverses for 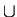 ? What are these inverses?
? What are these inverses?
- b
- Which subsets
 of
of
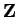 have inverses for
have inverses for 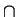 ? What are these inverses?
? What are these inverses?
2.12
Entertainment.
Let

be a set, and let
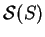
be the set of all subsets of

. Define a
binary operation
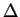
on
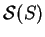
by
Thus
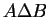
consists of all points that are in exactly one of the sets
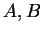
.
We call
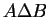
the
symmetric difference of

and
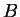
. Show that there
is an identity element for
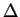
, and that every element of
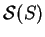
is
invertible for
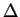
.
2.13
Definition (Associative operation.)
Let

be a binary operation on a set

. We say that

is
associative if
2.14
Examples.
Both
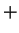
and
are associative operations on
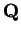
. Subtraction
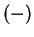
is not an associative operation on
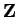
, since
Observe that to show that a binary operation

on a set

is not associative,
it is sufficient to find one point
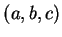
in
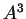
such that
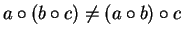
.
You should convince yourself that both 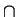 and
and 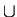 are associative operations
on the set
are associative operations
on the set
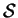 of all sets. If
of all sets. If 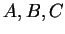 are sets, then
are sets, then
2.15
Theorem (Uniqueness of inverses.)
Let  be an associative operation on a set
be an associative operation on a set  , and suppose that there is an
identity
, and suppose that there is an
identity 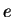 for
for  . Let
. Let 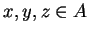 . If
. If 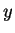 and
and 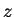 are inverses for
are inverses for  ,
then
,
then 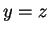 .
.
Proof: Since 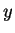 and
and 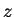 are inverses for
are inverses for  , we have
, we have
and
Hence,
2.16
Definition (Invertible element.)
Let

be a binary operation on a set

, having an identity element
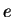
. I
will say that an element
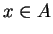
is
invertible for

, if

has an
inverse. If

is associative, then every invertible element for

has a
unique inverse, which I call
the inverse for  under
under 
.
2.17
Theorem (Double inverse theorem.)
Let  be an associative binary operation on a set
be an associative binary operation on a set  , with identity
, with identity 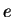 , and let
, and let
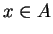 . If
. If  is invertible for
is invertible for  , let
, let 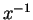 denote the
(unique) inverse for
denote the
(unique) inverse for  . Then
. Then 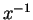 is invertible and
is invertible and
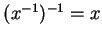 .
.
Proof: If 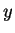 is the inverse for
is the inverse for  , then
, then
But this is exactly the condition for  to be the inverse for
to be the inverse for 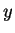 .
.

2.18
Examples.
As special cases of the double inverse theorem, we have
and
Here, as usual,
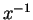
denotes the multiplicative inverse for

.
Proof: Let 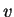 be invertible, and let
be invertible, and let 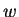 be the inverse for
be the inverse for 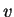 . Then for
all
. Then for
all 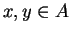 ,
,
This proves (2.20). The proof of (2.21) is left to you.
2.22
Exercise.
Prove the second half of the cancellation theorem.
2.29
Entertainment.
Is it possible to find integers
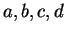
such that the five numbers
(
2.24)-(
2.28) are all different? If so, find four such integers.
2.30
Exercise.
Let

be an associative binary
operation on a set

,
and let
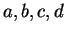
be elements of

.
- a)
- Show that there are five different ways to sensibly put parentheses in the
expression
and that all five ways produce the same result. (Each way will use two sets of
parentheses, e.g.
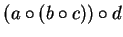 is one way. If you
arrange things correctly, you will just need to apply the associative law four times.)
is one way. If you
arrange things correctly, you will just need to apply the associative law four times.)
- b)
- Show that if
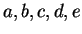 are elements of
are elements of  , then there are 14 ways to put
parentheses in
, then there are 14 ways to put
parentheses in
and that all 14 ways lead to the same result. Here each sensible way of inserting
parentheses will involve three pairs.
2.31
Entertainment.
Show that there are 42 ways to put parentheses in
This can be done without actually writing down all the ways (and there isn't much
point in writing down all the ways, because no one would read it if you did). If you
did part b. of the previous exercise in such a way that really showed that there are
just 14 ways, you should be able to do this, and then to calculate the number of ways
to parenthesize products with seven factors. There is a simple (but hard to guess)
formula for the number of ways to put parentheses in products with

factors. You
can find the formula, along with a derivation, in [
44].
2.32
Definition (Commutative operation.)
Let

be a binary operation on a set

. We say that

is
commutative if
2.33
Examples.
Both
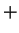
and
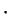
are commutative operations on
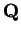
. However
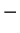
is not
a commutative operation on
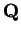
, because
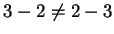
.
The operations 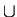 and
and 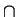 are both commutative operations on the set
are both commutative operations on the set
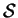 of
all sets, and and and or are commutative operations on the set
of
all sets, and and and or are commutative operations on the set
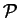 of
all propositions. The set difference operation
of
all propositions. The set difference operation 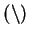 is not commutative on
is not commutative on
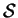 , since
, since




Next: 2.2 Some Examples
Up: 2. Fields
Previous: 2. Fields
Index
![]() be the set of all sets.2.1 Then union
be the set of all sets.2.1 Then union ![]() and intersection
and intersection ![]() and set
difference
and set
difference ![]() are binary operations on
are binary operations on
![]() .
.
![]() be the set of all propositions. Then and and or are binary
operations on
be the set of all propositions. Then and and or are binary
operations on
![]() . In mathematical logic, and is usually represented by
. In mathematical logic, and is usually represented by ![]() or
or ![]() ,
and or is represented by
,
and or is represented by ![]() or
or ![]() .
.
![]() be identity elements for
be identity elements for ![]() . Then
. Then
![]() on
on
![]() , the only element that has an inverse is
, the only element that has an inverse is ![]() ;
; ![]() is
its own inverse.
is
its own inverse.
![]() on
on
![]() , the only invertible elements are
, the only invertible elements are ![]() and
and ![]() . Both of these elements are equal to their own inverses.
. Both of these elements are equal to their own inverses.
![]() is any binary operation with identity
is any binary operation with identity ![]() , then
, then ![]() , so
, so ![]() is
always invertible, and
is
always invertible, and ![]() is equal to its own inverse.
is equal to its own inverse.
![]() and
and ![]() are associative operations
on the set
are associative operations
on the set
![]() of all sets. If
of all sets. If ![]() are sets, then
are sets, then
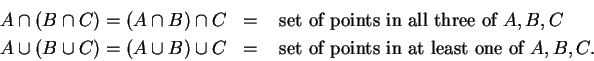
![]() and
and ![]() are inverses for
are inverses for ![]() , we have
, we have
![]() is the inverse for
is the inverse for ![]() , then
, then
![]() be invertible, and let
be invertible, and let ![]() be the inverse for
be the inverse for ![]() . Then for
all
. Then for
all ![]() ,
,
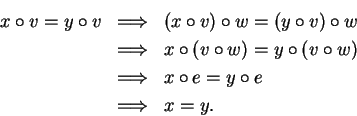
![]() and
and ![]() are both commutative operations on the set
are both commutative operations on the set
![]() of
all sets, and and and or are commutative operations on the set
of
all sets, and and and or are commutative operations on the set
![]() of
all propositions. The set difference operation
of
all propositions. The set difference operation ![]() is not commutative on
is not commutative on
![]() , since
, since