Next: 14. The Inverse Function
Up: 13. Applications
Previous: 13.2 Optimization Problems.
Index
13.3 Rates of Change
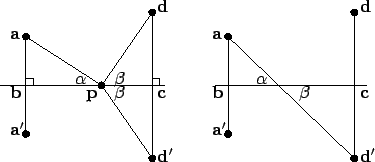
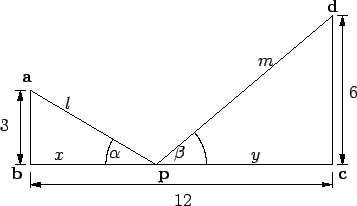
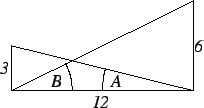
Suppose in the given figure, I want to find the shortest path from
a to a point p on the segment
![$[\mbox{{\bf b}} \mathbf{{\bf c}}]$](img3381.gif) and back to
d. Any such path will be uniquely defined by giving any one of the six
numbers:
and back to
d. Any such path will be uniquely defined by giving any one of the six
numbers:
Here  are as shown in the figure below:
are as shown in the figure below:
For a given point p, any of the six numbers
is a
function of any of the others. For example, we have 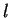 is a function of
is a function of 
and 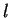 is a function of
is a function of 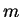 , since for
, since for ![$x\in [0,12]$](img3386.gif) and
and ![$y\in [0,12]$](img3387.gif) we have
we have
Also 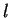 is a function of
is a function of 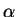 , since by similar triangles
, since by similar triangles
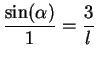 and hence
and hence
We have
and
I refer to
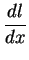 as the rate of change of
as the rate of change of 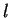 with respect to
with respect to  and to
and to
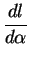 as the rate of
change of
as the rate of
change of
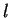 with respect to
with respect to 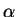 . Note that the ``
. Note that the `` 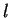 "'s in ``
"'s in ``
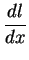 '' and ``
'' and ``
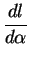 ''
represent
different functions. In the first case
''
represent
different functions. In the first case
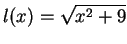 and in the
second
case
and in the
second
case
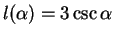 . Here
. Here
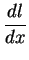 is positive,
indicating that
is positive,
indicating that 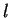 increases when
increases when  increases, and
increases, and
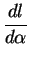 is negative, indicating that
is negative, indicating that 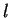 decreases when
decreases when 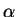 increases.
increases.
I want to find the path for which 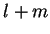 is shortest; i.e., I want to find the
minimum value of
is shortest; i.e., I want to find the
minimum value of 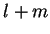 . I can think of
. I can think of 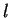 and
and 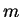 as being functions of
as being functions of  ,
and
then the minimum value will occur when
,
and
then the minimum value will occur when
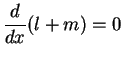 ; i.e.,
; i.e.,
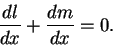 |
(13.16) |
Now 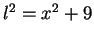 , so
, so
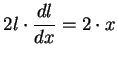 ; i.e.,
; i.e.,
and
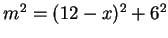 , so
, so
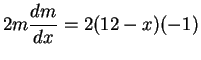 , i.e.,
, i.e.,
Equation (13.16) thus says that for the minimum path
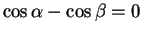 ; i.e.,
; i.e.,
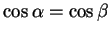 , and hence
, and hence
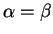 .
Thus the minimizing path satisfies the reflection condition, angle of
incidence
equals angle of reflection. Hence the minimizing triangle will make
.
Thus the minimizing path satisfies the reflection condition, angle of
incidence
equals angle of reflection. Hence the minimizing triangle will make
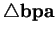 and
and
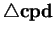 similar, and will satisfy
similar, and will satisfy
so
or
This example was done pretty much as
Leibniz would have done it. You should compare
the solution given here to your solution of exercise 13.15A.
The problem in the last example was solved by Heron (date uncertain, sometime
between 250 BC and 150 AD)
as follows[26, page 353].
Imagine the line
![$[{\bf b}{\bf c}]$](img3414.gif) to be a mirror. Let
to be a mirror. Let 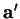 and
and
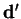 denote the images of
denote the images of 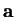 and
and 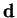 in the mirror,
in the mirror,
i.e. ![$[{\bf aa}']$](img3420.gif) and
and ![$[{\bf dd}']$](img3421.gif) are perpendicular to
are perpendicular to ![$[{\bf bc}]$](img3422.gif) and dist
and dist
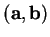 = dist
= dist
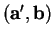 , dist
, dist
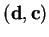 = dist
= dist
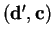 . Consider any path
. Consider any path 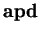 going from
a to a point p on the mirror, and then to d.
Then triangle
going from
a to a point p on the mirror, and then to d.
Then triangle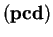 and triangle
and triangle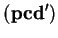 are congruent, and hence
are congruent, and hence
and hence the paths apd and 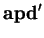 have equal lengths.
Now the shortest path
have equal lengths.
Now the shortest path 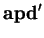 is a straight line, which makes
the angles
is a straight line, which makes
the angles 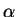 and
and 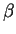 are vertical angles, which are equal.
Hence the shortest path makes the angle of incidence equal to
the angle of reflection, as we found above by calculus.
are vertical angles, which are equal.
Hence the shortest path makes the angle of incidence equal to
the angle of reflection, as we found above by calculus.
Remark: We can think of velocity as being rate of change of position with
respect
to time.
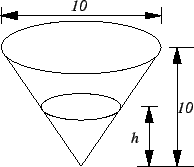
13.17
Exercise.
Consider a conical tank in the shape of a right circular cone with
altitude
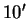
and
diameter
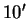
as shown in the figure.
Water flows into the tank at a constant rate of 10 cubic ft./minute. Let
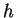
denote
the height of the water in the tank at a given time

. Find the rate of
change of
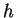
with respect to

. What is this rate when the height of the water is
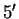
?
What can you say about
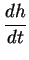
when
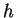
is nearly
zero?
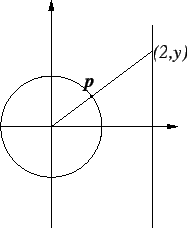
13.18
Exercise.
A particle
p moves on the rim of a
wheel
of radius 1 that rotates about the origin at constant angular speed
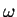
, so that
at time

it is at the point
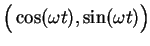
. A light at
the
origin causes
p to cast a shadow at the
point
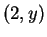
on a wall two feet from the center of the wheel.
Find the rate of
change of
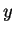
with respect to time. You should ignore the speed of light, i.e.
ignore the time it takes light to travel from the origin to the wall.




Next: 14. The Inverse Function
Up: 13. Applications
Previous: 13.2 Optimization Problems.
Index
Ray Mayer
2007-09-07

![]() and back to
d. Any such path will be uniquely defined by giving any one of the six
numbers:
and back to
d. Any such path will be uniquely defined by giving any one of the six
numbers:
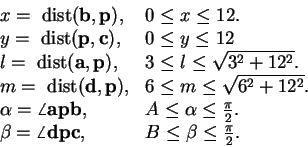
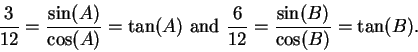
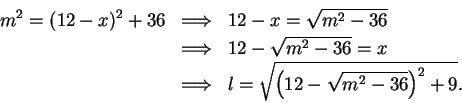
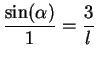 and hence
and hence
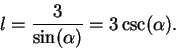
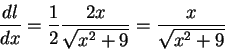
![]() is shortest; i.e., I want to find the
minimum value of
is shortest; i.e., I want to find the
minimum value of ![]() . I can think of
. I can think of ![]() and
and ![]() as being functions of
as being functions of ![]() ,
and
then the minimum value will occur when
,
and
then the minimum value will occur when
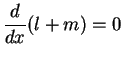 ; i.e.,
; i.e.,
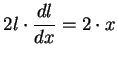 ; i.e.,
; i.e.,
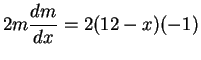 , i.e.,
, i.e.,
![]() ; i.e.,
; i.e.,
![]() , and hence
, and hence
![]() .
Thus the minimizing path satisfies the reflection condition, angle of
incidence
equals angle of reflection. Hence the minimizing triangle will make
.
Thus the minimizing path satisfies the reflection condition, angle of
incidence
equals angle of reflection. Hence the minimizing triangle will make
![]() and
and
![]() similar, and will satisfy
similar, and will satisfy
![]() to be a mirror. Let
to be a mirror. Let ![]() and
and
![]() denote the images of
denote the images of ![]() and
and ![]() in the mirror,
in the mirror,