



Next: 8.2 Properties of the
Up: 8. Integrable Functions
Previous: 8. Integrable Functions
Index
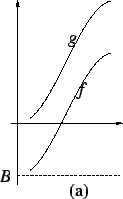
If  is a monotonic function from an interval
is a monotonic function from an interval ![$[a,b]$](img1071.gif) to
to
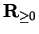 ,
then we
have shown that for every sequence
,
then we
have shown that for every sequence 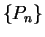 of partitions on
of partitions on ![$[a,b]$](img1071.gif) such that
such that
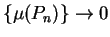 , and every sequence
, and every sequence 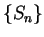 such that
for all
such that
for all
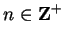
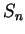 is a sample for
is a sample for 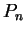 ,
we have
,
we have
8.1
Definition (Integral.)
Let

be a bounded function from an interval
![$[a,b]$](img1071.gif)
to
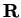
. We say that

is
integrable on ![$[a,b]$](img1071.gif)
if there is a number
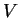
such that for every sequence of partitions
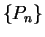
on
![$[a,b]$](img1071.gif)
such that
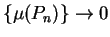
, and every sequence
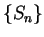
where
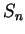
is a sample for
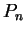
If

is integrable on
![$[a,b]$](img1071.gif)
then the number
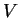
just described is denoted
by
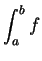
and is called `` the integral from

to

of

.''
Notice that by our definition an integrable function is necessarily
bounded.
The definition just given is essentially due to Bernhard Riemann(1826-1866),
and
first appeared around 1860[39, pages 239 ff]. The symbol
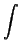 was introduced by Leibniz sometime around 1675[15, vol 2, p242]. The symbol is a form of the letter s, standing for sum
(in Latin as well as in English.) The practice of attaching the
limits
was introduced by Leibniz sometime around 1675[15, vol 2, p242]. The symbol is a form of the letter s, standing for sum
(in Latin as well as in English.) The practice of attaching the
limits  and
and  to the integral sign was introduced by Joseph Fourier
around 1820. Before this time the limits were usually indicated
by words.
to the integral sign was introduced by Joseph Fourier
around 1820. Before this time the limits were usually indicated
by words.
We can now restate theorems 7.6 and 7.15 as follows:
In general integrable functions may take negative as well as positive values
and in
these cases
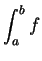 does not represent an area.
does not represent an area.
The next theorem shows that monotonic functions are integrable even if
they take on negative values.
8.4
Example (Monotonic functions are integrable II.)
Let

be a
monotonic function from an interval
![$[a,b]$](img1071.gif)
to
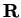
. Let
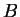
be a non-positive number such that
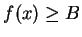
for all
![$x\in [a,b]$](img1976.gif)
. Let
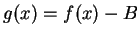
.
Then

is a monotonic function from
![$[a,b]$](img1071.gif)
to
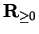
.
Hence by theorem
7.6,

is integrable on
![$[a,b]$](img1071.gif)
and
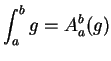
. Now let
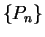
be a sequence of partitions of
![$[a,b]$](img1071.gif)
such that
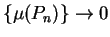
, and let
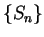
be a sequence such that for each

in
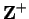
,
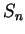
is a sample for
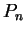
. Then
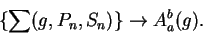 |
(8.5) |
If
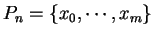
and
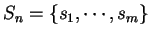
then
Thus by (
8.5)
If we use the fact that
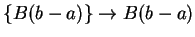
, and then use the sum theorem
for limits of sequences, we get
It follows from the definition of integrable functions that

is integrable
on
![$[a,b]$](img1071.gif)
and
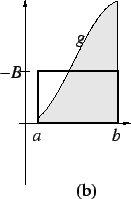
Thus in figure b,
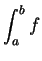 represents the shaded area with the area of
the
thick box subtracted from it, which is the same as the area of the region
marked ``
represents the shaded area with the area of
the
thick box subtracted from it, which is the same as the area of the region
marked `` " in figures c and d, with the area of the region marked
``
" in figures c and d, with the area of the region marked
``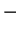 "
subtracted from it.
"
subtracted from it.
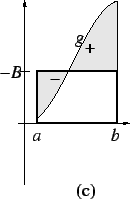
The figure represents a geometric interpretation for a Riemann sum. In the
figure
is the area of
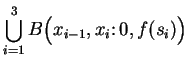 and
and
is the negative of the area of
In general you should think of
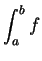 as the difference
as the difference
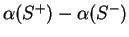 where
where
and
8.7
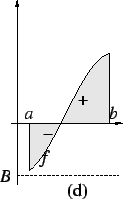
Exercise.
Below is the graph of a function

.
By looking at the graph of

estimate the following integrals.
(No explanation is necessary.)
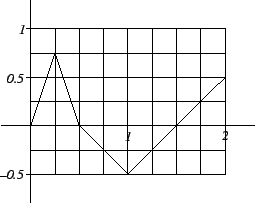
Graph of

- a)
-
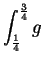 .
.
- b)
-
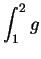 .
.
- c)
-
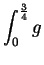 .
.




Next: 8.2 Properties of the
Up: 8. Integrable Functions
Previous: 8. Integrable Functions
Index
Ray Mayer
2007-09-07
![]() was introduced by Leibniz sometime around 1675[15, vol 2, p242]. The symbol is a form of the letter s, standing for sum
(in Latin as well as in English.) The practice of attaching the
limits
was introduced by Leibniz sometime around 1675[15, vol 2, p242]. The symbol is a form of the letter s, standing for sum
(in Latin as well as in English.) The practice of attaching the
limits ![]() and
and ![]() to the integral sign was introduced by Joseph Fourier
around 1820. Before this time the limits were usually indicated
by words.
to the integral sign was introduced by Joseph Fourier
around 1820. Before this time the limits were usually indicated
by words.
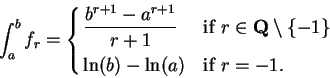
![]() does not represent an area.
does not represent an area.
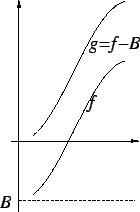
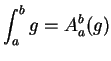 . Now let
. Now let
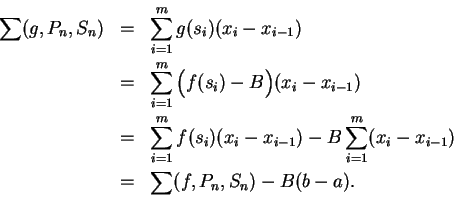
![]() represents the shaded area with the area of
the
thick box subtracted from it, which is the same as the area of the region
marked ``
represents the shaded area with the area of
the
thick box subtracted from it, which is the same as the area of the region
marked ``![]() " in figures c and d, with the area of the region marked
``
" in figures c and d, with the area of the region marked
``![]() "
subtracted from it.
"
subtracted from it.
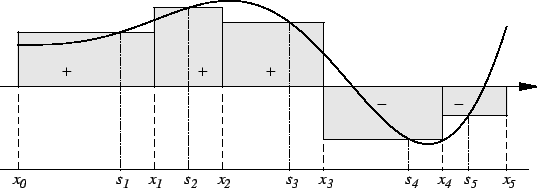
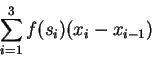
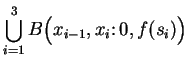 and
and
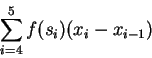
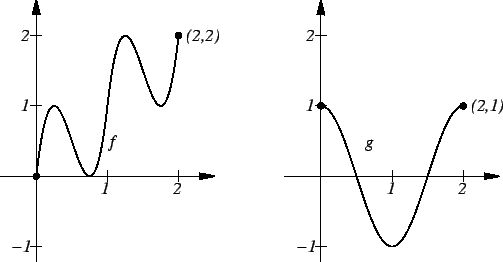
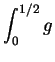 or
or
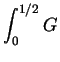 ?
?

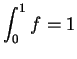 .
.
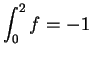 .
.
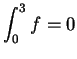 .
.
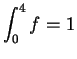 .
.