



Next: 8. Integrable Functions
Up: 7. Still More Area
Previous: 7.1 Area Under a
Index
Proof: Let  be a generic element of
be a generic element of
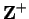 . To simplify the
notation, I will write
. To simplify the
notation, I will write
Let
and let
Then for 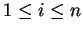
so
It follows by the  th root rule (theorem 6.48)
that
th root rule (theorem 6.48)
that
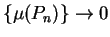 .
Hence it follows from theorem 7.6 that
.
Hence it follows from theorem 7.6 that
![\begin{displaymath}
A_1^a[t^r]=\lim\Big(\sum
([t^r],P_n,S_n)\Big).
\end{displaymath}](img1895.gif) |
(7.8) |
Now
Here we have used the formula for a finite geometric series. Thus, from
(7.8)
Now we want to calculate the limit appearing in the previous lemma. In order
to do this it will be convenient to prove a few general limit theorems.
Proof: Suppose 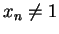 for all
for all  , and
, and 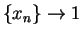 .
.
Case 1: Suppose 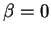 . Then the conclusion clearly follows.
. Then the conclusion clearly follows.
Case 2: Suppose
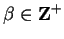 . Then by the formula for a geometric series
. Then by the formula for a geometric series
By the sum theorem and many applications of the product theorem
we conclude that
Case 3: Suppose
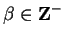 . Let
. Let
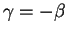 . Then
. Then
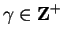 ,
so
by Case 2 we get
,
so
by Case 2 we get
Case 4: Suppose
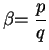 where
where
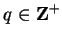 and
and
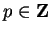 .
Let
.
Let
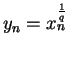 . Then
. Then
Now if we could show that 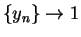 , it would follow from this formula
that
, it would follow from this formula
that
The next lemma shows that 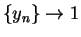 and completes the proof of theorem
7.10.
and completes the proof of theorem
7.10.
7.11
Lemma.
Let 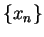 be a sequence of positive numbers such that
be a sequence of positive numbers such that 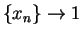 , and
, and
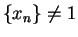 for all
for all
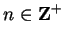 . Then
for each
. Then
for each 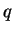 in
in
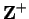 ,
,
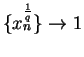 .
.
Proof: Let 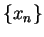 be a sequence of positive numbers such that
be a sequence of positive numbers such that 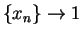 .
Let
.
Let
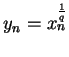 for each
for each  in
in
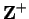 . We want to show that
. We want to show that
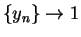 . By the formula for a finite geometric series
. By the formula for a finite geometric series
so
Now
Since 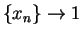 , we have
, we have
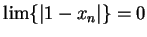 , so by the
squeezing rule
, so by the
squeezing rule
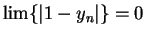 , and hence
, and hence
Proof: By lemma 7.7,
By theorem 7.10,
and putting these results together, we get
7.13
Lemma.
Let
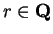 , and let
, and let
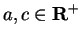 , with
, with 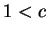 . Then
. Then
Proof: If
is a partition of ![$[1,c]$](img1942.gif) , let
, let
be the partition of ![$[a,ca]$](img1944.gif) obtained by multiplying the points of
obtained by multiplying the points of  by
by  .
Then
.
Then
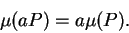 |
(7.14) |
If
is a sample for  , let
, let
be the corresponding sample for 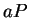 .
Then
.
Then
Let 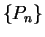 be a sequence of partitions of
be a sequence of partitions of ![$[1,c]$](img1942.gif) such that
such that
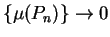 , and for each
, and for each
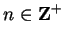 let
let 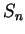 be a sample for
be a sample for
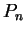 . It follows from (7.14) that
. It follows from (7.14) that
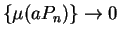 .
By the area theorem for monotonic functions (theorem 7.6),
we have
.
By the area theorem for monotonic functions (theorem 7.6),
we have
Thus
Proof: The result for the case 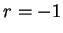 was proved in theorem 5.76.
The case
was proved in theorem 5.76.
The case 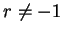 is done in the following exercise.
is done in the following exercise.
7.16
Exercise.
A
Use the two previous lemmas to prove
theorem
7.15 for the case
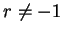
.
Remark: In the proof of lemma 7.7, we did not use the assumption
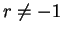 until line (7.9). For
until line (7.9). For 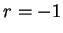 equation (7.9)
becomes
equation (7.9)
becomes
Since in this case
![$\displaystyle {\{\sum ([t^{-1}],P_n,S_n)\}\to A_1^a[{1\over t}]=\ln
(a)}$](img1958.gif) ,we conclude that
,we conclude that
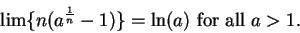 |
(7.17) |
This formula give us method of calculating
logarithms by taking square roots.
We
know
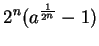 will be near to
will be near to 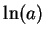 when
when  is
large,
and
is
large,
and
 can be calculated by taking
can be calculated by taking  successive
square
roots. On my calculator, I pressed the following sequence of keys
successive
square
roots. On my calculator, I pressed the following sequence of keys
and got the result 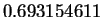 . My calculator also says that
. My calculator also says that
 . It appears that if I know how to calculate square roots, then
I
can calculate logarithms fairly easily.
. It appears that if I know how to calculate square roots, then
I
can calculate logarithms fairly easily.
7.18
Exercise.
A
Let
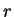
be a non-negative rational number, and let
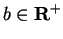
. Show that
Where in your proof do you use the fact
that
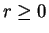
?




Next: 8. Integrable Functions
Up: 7. Still More Area
Previous: 7.1 Area Under a
Index
Ray Mayer
2007-09-07
![\begin{displaymath}A_1^a[t^r]=(a^{r+1}-1)\lim\left\{ {{a^{1\over n}-1}\over {a^{{r+1}\over
n}-1}}\right\}.\end{displaymath}](img1889.gif)
![\begin{displaymath}A_1^a[t^r]=(a^{r+1}-1)\lim\left\{ {{a^{1\over n}-1}\over {a^{{r+1}\over
n}-1}}\right\}.\end{displaymath}](img1889.gif)
![]() be a generic element of
be a generic element of
![]() . To simplify the
notation, I will write
. To simplify the
notation, I will write
![\begin{eqnarray*}
A_1^a[t^r]&=&\lim \Big\{ (a^{r+1}-1) {{(a^{{1\over n}}-1)}\ove...
...}\over {a^{ {{r+1}\over n}
}-1}} \right\}.\mbox{ $\diamondsuit$}
\end{eqnarray*}](img1902.gif)
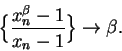
![]() for all
for all ![]() , and
, and ![]() .
.
![]() . Then the conclusion clearly follows.
. Then the conclusion clearly follows.
![]() . Then by the formula for a geometric series
. Then by the formula for a geometric series
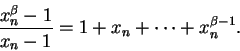
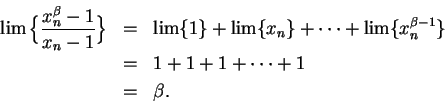
![]() . Let
. Let
![]() . Then
. Then
![]() ,
so
by Case 2 we get
,
so
by Case 2 we get
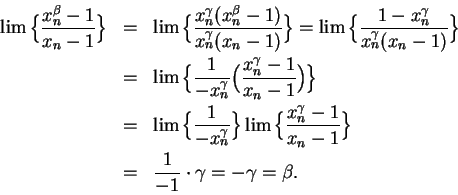
![]() where
where
![]() and
and
![]() .
Let
.
Let
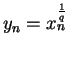 . Then
. Then
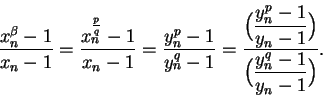
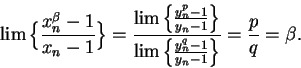
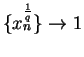 .
.
![]() be a sequence of positive numbers such that
be a sequence of positive numbers such that ![]() .
Let
.
Let
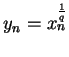 for each
for each ![]() in
in
![]() . We want to show that
. We want to show that
![]() . By the formula for a finite geometric series
. By the formula for a finite geometric series
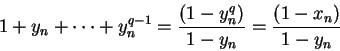
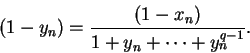
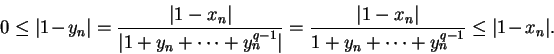
![\begin{displaymath}A_1^b[t^r] =
{b^{r+1}-1\over r+1}.\end{displaymath}](img1934.gif)
![\begin{displaymath}A_1^b[t^r]=(b^{r+1}-1)\lim\Big\{ {{b^{{1\over n}}-1}\over {b^{ {{r+1}\over
n}}-1}}\Big\}.\end{displaymath}](img1935.gif)
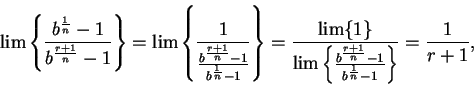
![\begin{displaymath}A_1^b[t^r]={{b^{r+1}-1}\over {r+1}}.\mbox{ $\diamondsuit$}\end{displaymath}](img1937.gif)
![\begin{eqnarray*}
\sum([t^r],aP,aS) &=& \sum_{i=1}^n (as_i)^r(ax_i - ax_{i-1})\\...
...um_{i=1}^n s_i^r (x_i - x_{i-1})\\
&=& a^{r+1} \sum([t^r],P,S).
\end{eqnarray*}](img1949.gif)
![\begin{eqnarray*}
A_a^{ca}[t^r] &=& \lim \{ \sum([t^r],aP_n,aS_n) \} \\
&=& \li...
...r],P_n,S_n) \} \\
&=& a^{r+1}A_1^c[t^r]. \mbox{ $\diamondsuit$}
\end{eqnarray*}](img1952.gif)
![]() until line (7.9). For
until line (7.9). For ![]() equation (7.9)
becomes
equation (7.9)
becomes
![$\displaystyle {\{\sum ([t^{-1}],P_n,S_n)\}\to A_1^a[{1\over t}]=\ln
(a)}$](img1958.gif) ,we conclude that
,we conclude that
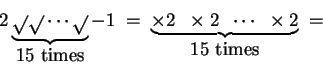
![\begin{displaymath}{
A_0^b[t^r]={{b^{r+1}}\over {r+1}}}.\end{displaymath}](img1966.gif)