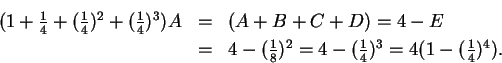For each ![]() in
in
![]() let
let ![]() denote the box
denote the box
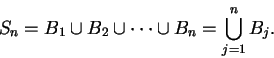
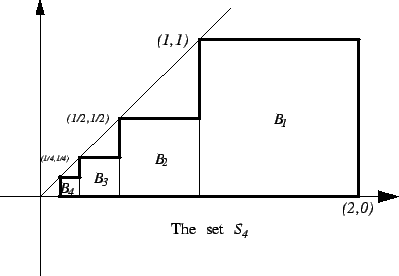
I want to find the area of ![]() . I have
. I have
Proof:
Let
Remark: Theorem 2.22 is very important, and you should remember it. Some people find it easier to remember the proof than to remember the formula. It would be good to remember both.
If we let
![]() in (2.23), then from equation (2.20)
we
obtain
in (2.23), then from equation (2.20)
we
obtain
Here ![]() ,
, ![]() ,
, ![]() , and
, and ![]() is the
point where the line
is the
point where the line ![]() intersects the line
intersects the line ![]() .
All of the points
.
All of the points ![]() lie on the line
lie on the line ![]() , and all of the points
, and all of the points
![]() lie on the line
lie on the line ![]() .
All of the segments
.
All of the segments ![]() are horizontal, and all segments
are horizontal, and all segments
![]() are parallel to
are parallel to ![]() . Show that the area of
. Show that the area of ![]() is
is
![]() . You will probably need to use the formula for a geometric
series.
. You will probably need to use the formula for a geometric
series.
(b) Find the number
(You may use a calculator, but you can probably do this without using a calculator.)
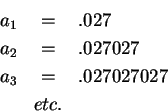
The Babylonians[45, page 77] knew that
Euclid knew a version of the formula for a finite geometric
series in the case where ![]() is a positive integer.
is a positive integer.
Archimedes knew the sum of the finite geometric series
when ![]() .
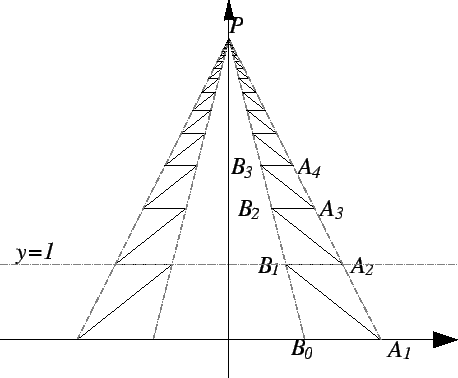
The idea of Archimedes' proof is illustrated
in the figure.
.
The idea of Archimedes' proof is illustrated
in the figure.
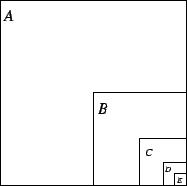
If the large square has side equal to ![]() , then
, then
![\begin{displaymath}\begin{array}{rll}
A& & = A \hspace{1em} = 3\\
\frac{1}{4}A...
...[1ex]
(\frac{1}{4})^3 A & = \frac{1}{4} C & = D.\\
\end{array}\end{displaymath}](img375.gif)