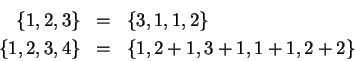Index

1.1 Sets

The ideas discussed in this chapter (e.g. set, proposition, function) are so basic that I cannot define them in terms of simpler ideas. Logically they are undefined concepts, even though I give definitions for them. My ``definitions'' use undefined words (e.g. collection, statement, rule) that are essentially equivalent to what I attempt to define. The purpose of these ``definitions'' and examples is to illustrate how the ideas will be used in the later chapters. I make frequent use of the undefined terms ``true'', ``false'', and ``there is''. It might be appropriate to spend some time discussing various opinions about the meaning of `` truth" and `` existence" in mathematics, but such a discussion would be more philosophical than mathematical, and would not be very relevant to anything that follows. If such questions interest you, you might enjoy reading Philosophy of Mathematics by Benacerraf and Putnam [7] or the article Schizophrenia in Contemporary Mathematics by Errett Bishop [10, pp 1-10]

Some of the terms and notation used in the examples in this chapter will be defined more precisely later in the notes. In this chapter I will assume familiar properties of numbers that you have used for many years.

1.1   Definition (Set.) A set is a collection of objects. A small set is often described by listing the objects it contains inside curly brackets, e.g.,

$$\{1,3,5,7,9\}$$

denotes the set of positive odd integers smaller than ten.

1.2   Notation ( $\mbox{{\bf N}}, \mbox{{\bf Z}}, \mbox{{\bf Q}}, \emptyset$.) A few sets appear so frequently that they have standard names:

$$\begin{eqnarray*} \mbox{{\bf N}}&=& \mbox{ set of natural numbers } = \{0,1,2,3,... ... \mbox{ empty set } =\{\;\}= \mbox{ set containing no objects. } \end{eqnarray*}$$

1.3   Notation ($\in, \not\in$.) If $A$ is a set and $a$ is an object, we write

$$a\in A$$

(read this as ``$a$ is in $A$") to mean that $a$ is an object in $A$, and we write

$$a\notin A$$

(read this as ``$a$ is not in $A$") to mean that $a$ is not in $A$.

1.4   Example. Thus we have

$$2 \in \mbox{{\bf Z}}, \mbox{{}}$$

$$-2 \notin \mbox{{\bf N}}, \mbox{{}}$$

$$2 \in \{1,2,5\} \mbox{{}}$$

$$\{1,2\} \notin \{1,2,5\}.$$ (1.5)

To see why (1.5) is true, observe that the only objects in $\{1,2,5\}$ are $1$, $2$, and $5$. Since

$$\{1,2\}\neq 1 \mbox{ and } \{1,2\}\neq 2 \mbox{ and } \{1,2\}\neq 5$$

it follows that $\{1,2\}\notin \{1,2,5\}$.

1.6   Definition (Subset, $\subset$.) Let $A$ and $B$ be sets. We say that $A$ is a subset of $B$ and write

$$A\subset B$$

if and only if every object in $A$ is also in $B$.

1.7   Example.

$$\begin{eqnarray*} \mbox{{\bf N}}&\subset& \mbox{{\bf Z}}, \\ \emptyset &\subset... ...\{1,2\} &\subset& \{1,2,3\}, \\ \{1\} &\subset& \mbox{{\bf Z}}, \end{eqnarray*}$$

are all true statements. However

$$1\subset\mbox{{\bf Z}}$$ (1.8)

is not a statement, but an ungrammatical phrase, since $A\subset B$ has only been defined when $A$ and $B$ are sets, and $1$ is not a set.

1.9   Definition (Set equality.) Two sets $A$ and $B$ are considered to be the same if and only if they contain exactly the same objects. In this case we write

$$A=B.$$

Thus $A=B$ if and only if $A\subset B$ and $B \subset A$.

1.10   Example.

$$\begin{eqnarray*} \{1,2,3\} &=& \{3,1,1,2\} \\ \{1,2,3,4\} &=& \{1,2+1,3+1,1+1,2+2\} \end{eqnarray*}$$