1.57
Definition (Function.)
Let
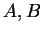
be sets, and let

be a rule that assigns to each element

in

a
unique element (denoted by
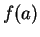
) in
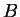
. The ordered triple
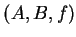
is called a
function with domain  and codomain
and codomain 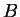
. We write
to indicate that
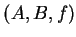
is a function. It follows from the definition that two
functions are equal if and only if they have the same domain, the same codomain, and
the same rule: If
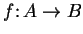
and
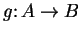
, I say that the rule

and
the rule
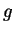
are the same if and only if
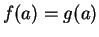
for all
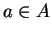
. We usually
say `` the function

" when we mean `` the function
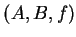
," i.e., we
name a function by giving just the name for its rule.
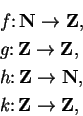
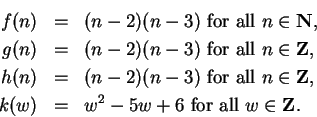
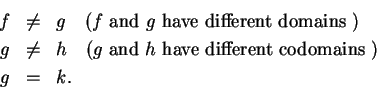
![]() is a proposition form on a set
is a proposition form on a set ![]() , then
, then ![]() determines a function whose
domain is
determines a function whose
domain is ![]() and whose codomain is the set of all propositions.
and whose codomain is the set of all propositions.