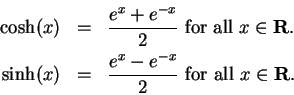Next: 15. The Second Derivative
Up: 14. The Inverse Function
Previous: 14.5 Inverse Function Theorems
Index
14.46
Example (Derivative of 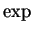 .)
.)
We know that
If we differentiate both sides of this equation, we get
i.e.
14.47
Example (Derivative of  )
)
Let
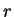
be any real number and
let
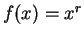
for all
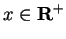
.
Then
so by the chain rule
(Here I have used the result of exercise
14.37.)
Thus the formula
which we have known for quite a while for rational exponents,
is actually valid for all real exponents.
14.48
Exercise (Derivative of 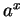 .)
.)
Let
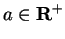
.
Show that
for all
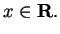
14.49
Example (Derivative of 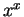 .)
.)
Hence
14.50
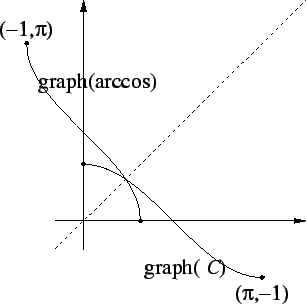
Example (Derivative of 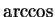 .)
.)
Let
![$C:[0,\pi] \to [-1,1]$](img3662.gif)
be defined by
We have
so
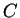
has an inverse function which is denoted by
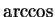
.
By the inverse function theorem
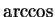
is differentiable on
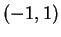
.
and we have
By the chain rule
Now since the sine function is positive on
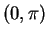
we get
for all
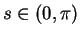
, so
Thus
14.51
Exercise (Derivative of 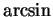 .)
.)
Let
Show that

has an inverse function that is differentiable on the
interior of its domain. This inverse functions is called
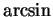
.
Describe the domain of
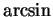
, sketch the graphs of

and of
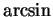
, and show that
14.52
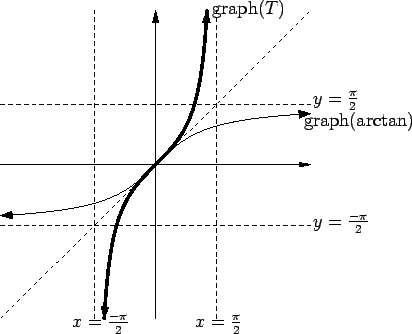
Example (Derivative of 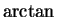 .)
.)
Let
Then T is continuous, and the image of
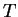
is unbounded both above
and below, so image(
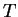
) =
R. Also
so
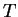
has an inverse function, which we denote by
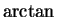
.
For all
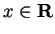
so by the chain rule
Now
so
Thus
14.53
Exercise (Derivative of arccot
.)
Let
Show that
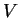
has an inverse function arccot, and that
What is
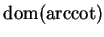
? Sketch the graphs of
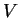
and of arccot.
Remark The first person to give a name to the
inverse trigonometric functions was Daniel Bernoulli (1700-1792)
who used 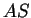 for
for 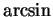 in 1729. Other early notations included
arc(cos. =
in 1729. Other early notations included
arc(cos. =  ) and ang(cos. =
) and ang(cos. =  )[15, page 175].
Many calculators and some calculus books use
)[15, page 175].
Many calculators and some calculus books use 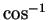 to denote
arccos. (If you use your calculator to find inverse trigonometric
functions, make sure that you set the degree-radian-grad mode to radians.)
to denote
arccos. (If you use your calculator to find inverse trigonometric
functions, make sure that you set the degree-radian-grad mode to radians.)
14.55
Exercise.
A
Let
Calculate the derivative of
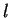
. What is the domain of this function?
Sketch the graph of
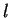
.
14.56
Exercise (Hyperbolic functions.)
We define functions
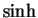
and
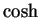
on
R by
These functions are called the
hyperbolic sine and the
hyperbolic
cosine respectively. Show that
and
Calculate
and simplify your answer as much as you can. What conclusion can you
draw from your answer? Sketch the graphs of
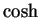
and
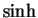
on
one set of coordinate axes.




Next: 15. The Second Derivative
Up: 14. The Inverse Function
Previous: 14.5 Inverse Function Theorems
Index
Ray Mayer
2007-09-07
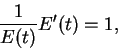
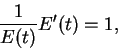
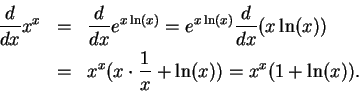
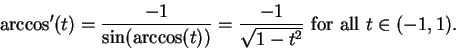
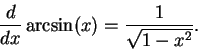
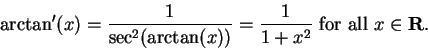
![]() for
for ![]() in 1729. Other early notations included
arc(cos. =
in 1729. Other early notations included
arc(cos. = ![]() ) and ang(cos. =
) and ang(cos. = ![]() )[15, page 175].
Many calculators and some calculus books use
)[15, page 175].
Many calculators and some calculus books use ![]() to denote
arccos. (If you use your calculator to find inverse trigonometric
functions, make sure that you set the degree-radian-grad mode to radians.)
to denote
arccos. (If you use your calculator to find inverse trigonometric
functions, make sure that you set the degree-radian-grad mode to radians.)
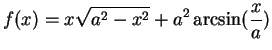 .
.
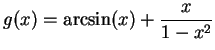 .
.
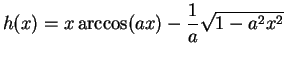 .
.