14.1 The Intermediate Value Property

14.1   Assumption (Intermediate value property 1.) Let $a,b$ be real numbers with $a<b$, and let $f$ be a continuous function from $[a,b]$ to R such that $f(a) < 0$ and $f(b) > 0$. Then there is some number $c\in (a,b)$ such that $f(c) = 0.$

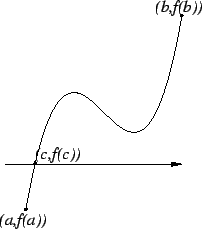
The intermediate value theorem was first proved in 1817 by Bernard Bolzano (1781-1848). However Bolzano published his proof in a rather obscure Bohemian journal, and his work did not become well known until much later. Before the nineteenth century the theorem was often assumed implicitly, i.e. it was used without stating that it was an assumption.

14.2   Definition ($c$ is between $a$ and $b$.) Let $a$, $b$ and $c$ be real numbers with $a\neq b$. We say that $c$ is between $a$ and $b$ if either $a < c < b$ or $b<c<a$.

14.3   Corollary (Intermediate value property 2.) Let $f$ be a continuous function from some interval $[a,b]$ to R, such that $f(a)$ and $f(b)$ have opposite signs. Then there is some number $c$ between $a$ and $b$ such that $f(c) = 0$.

Proof:     If $f(a) < 0 < f(b)$ the result follows from assumption 14.1. Suppose that $f(b) < 0 < f(a)$. Let $g(x) = -f(x)$ for all $x\in [a,b]$. then $g$ is a continuous function on $[a,b]$ and $g(a) < 0 < g(b)$. It follows that there is a number $c\in (a,b)$ such that $g(c) = 0$, and then $f(c) = -g(c) = 0.$ $\diamondsuit$

14.4   Corollary (Intermediate value property 3.) Let $a,b$ be real numbers with $a<b$, and let $f:[a,b] \to \mbox{{\bf R}}$ be a continuous function such that $f(a) \neq f(b)$. Let $p$ be any number between $f(a)$ and $f(b)$. Then there is a number $c\in (a,b)$ such that $f(c) = p$.

14.5   Exercise. A Prove Corollary 14.4. You may assume that $f(a) < f(b)$.