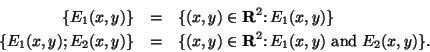
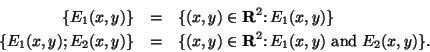

In this section we will discuss the idea of tangent to a curve and the related idea of velocity of a moving point.
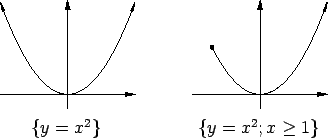
You probably have a pretty good intuitive idea of what is meant by the tangent to a curve, and you can see that the straight lines in figure a below represent tangent lines to curves.
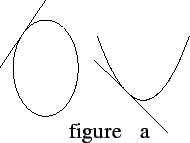
It may not be quite so clear what you would mean by the tangents to the
curves in figure b at the point ![]() .
.
Euclid (fl. c. 300 B.C.) defined a tangent to a circle to be a line which touches the circle in exactly one point. This is a satisfactory definition of tangent to a circle, but it does not generalize to more complicated curves.
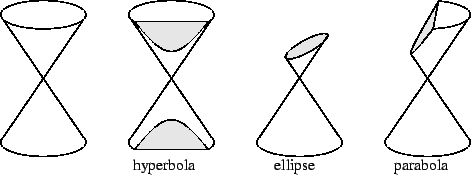
Apollonius (c 260-170 B.C.) defined a tangent to a conic section (i.e., an ellipse or hyperbola or parabola) to be a line that touches the section, but lies outside of the section. Apollonius considered these sections to be obtained by intersecting a cone with a plane, and points inside of the section were points in the cone.
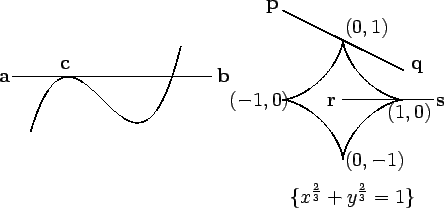
In the figure, the line ![]() ought to be tangent to the curve at
ought to be tangent to the curve at ![]() ,
but
there is no reasonable sense in which the line lies outside the curve.
On the other hand, it may not be clear whether
,
but
there is no reasonable sense in which the line lies outside the curve.
On the other hand, it may not be clear whether ![]() (which lies outside
the
curve
(which lies outside
the
curve
![]() is more of a tangent than the line
is more of a tangent than the line ![]() which does
not lie outside of it. Leibniz
[33, page 276]
said that
which does
not lie outside of it. Leibniz
[33, page 276]
said that
to find a tangent means to draw a line that connects two points of the curve at an infinitely small distance, or the continued side of a polygon with an infinite number of angles, which for us takes the place of the curve.
From a modern point of view it is hard to make any sense out of this.
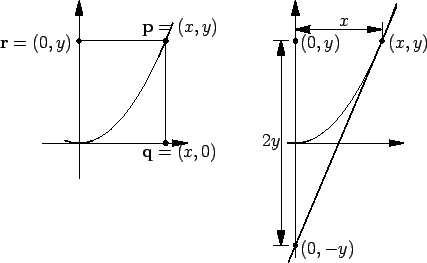
Here is a seventeenth century sort of argument for finding a tangent to the
parabola
whose equation is ![]() .
.
In The Analyst: A Discourse Addressed to an Infidel
Mathematician[7, page 73], George Berkeley (1685-1753)
criticizes the
argument above, pointing out that when we divide by ![]() in line (10.3)
we must assume
in line (10.3)
we must assume ![]() is not zero, and then at the end we set
is not zero, and then at the end we set ![]() equal to
equal to ![]() .
.
All which seems a most inconsistent way of arguing, and such as would not be allowed of in Divinity.The technical concept of velocity is not a simple one. The idea of uniform velocity causes no problems: to quote Galileo (1564-1642):
By steady or uniform motion, I mean one in which the distances traversed by the moving particle during any equal intervals of time, are themselves equal[21, page 154].This definition applies to points moving in a straight line, or points moving on a circle, and it goes back to the Greek scientists. The problem of what is meant by velocity for a non-uniform motion, however, is not at all clear. The Greeks certainly realized that a freely falling body moves faster as it falls, but they had no language to describe the way in which velocity changes. Aristotle (384-322 B.C.) says
there cannot be motion of motion or becoming of becoming or in general change of change[11, page 168].It may not be clear what this means, but S. Bochner interprets this as saying that the notion of a second derivative (this is a technical term for the mathematical concept used to describe acceleration which we will discuss later) is a meaningless idea[11, page 167]. Even though we are in constant contact with non-uniformly moving bodies, our intuition about the way they move is not very good. In the Dialogues Concerning Two New Sciences, Salviati (representing Galileo) proposes the hypothesis that if a stone falls from rest, then it falls in such a way that `` in any equal intervals of time whatever, equal increments of speed are given to it"[21, page 161].
In our language, the hypothesis is that the velocity ![]() at time
at time ![]() satisfies
satisfies
Earlier, in 1604, Galileo
had supposed that