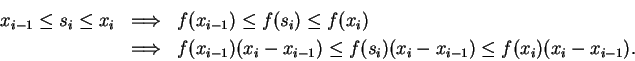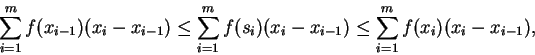Next: 7.2 Calculation of Area
Up: 7. Still More Area
Previous: 7. Still More Area
Index
7.1
Theorem.
Let  be a monotonic function from the interval
be a monotonic function from the interval ![$[a,b]$](img1071.gif) to
to
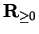 . Let
. Let 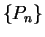 be a sequence of partitions of
be a sequence of partitions of ![$[a,b]$](img1071.gif) such
that
such
that
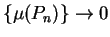 , and let
Then
and
(The notation here is the same as in theorem 5.40 and exercise
5.47.
, and let
Then
and
(The notation here is the same as in theorem 5.40 and exercise
5.47.
Proof: We noted in theorem 5.40 and exercise 5.47 that
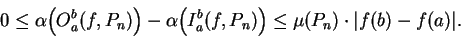 |
(7.2) |
Since
we conclude from the squeezing rule that
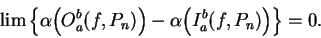 |
(7.3) |
We also have by (5.43) that
so that
By (7.3) and the squeezing rule
and hence
Also,
7.4
Definition (Riemann sum.)
Let
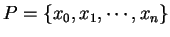
be a partition for an
interval
![$[a,b]$](img1071.gif)
. A
sample for

is a finite sequence
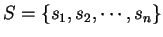
of numbers such that
![$s_i\in[x_{i-1},x_i]$](img1866.gif)
for
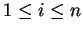
. If

is
a function from
![$[a,b]$](img1071.gif)
to
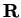
, and

is a partition for
![$[a,b]$](img1071.gif)
and

is
a
sample for

, we define
and
we call
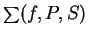
a
Riemann sum for
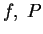
and

.
We will sometimes write
![$\sum([f(t)],P,S)$](img1870.gif)
instead of
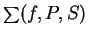
.
7.5
Example.
If

is an increasing function from
![$[a,b]$](img1071.gif)
to
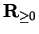
, and
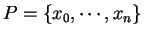
is a partition of
![$[a,b]$](img1071.gif)
, and
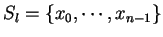
, then
If
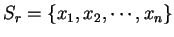
, then
If
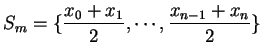
then
is some number between
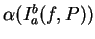
and
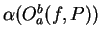
.
Proof: We will consider the case where  is increasing. The case where
is increasing. The case where  is
decreasing is similar.
is
decreasing is similar.
For each partition
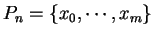 and sample
and sample
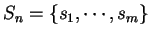 ,
we have for
,
we have for 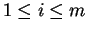
Hence
i.e.,
By theorem 7.1 we have
and
so by the squeezing rule,




Next: 7.2 Calculation of Area
Up: 7. Still More Area
Previous: 7. Still More Area
Index
Ray Mayer
2007-09-07
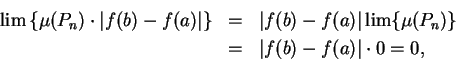
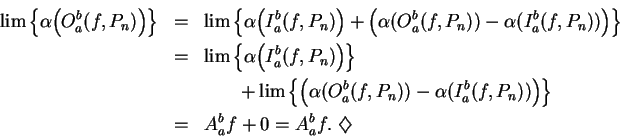
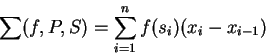
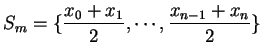 then
then
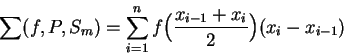
![]() is increasing. The case where
is increasing. The case where ![]() is
decreasing is similar.
is
decreasing is similar.
![]() and sample
and sample
![]() ,
we have for
,
we have for ![]()