In the first part of these notes we consider the problem of calculating
the areas of various plane figures.
The technique we use for finding the area of a figure ![]() will
be to construct a sequence
will
be to construct a sequence ![]() of sets contained in
of sets contained in ![]() , and a sequence
, and a sequence
![]() of sets containing
of sets containing ![]() , such that
, such that
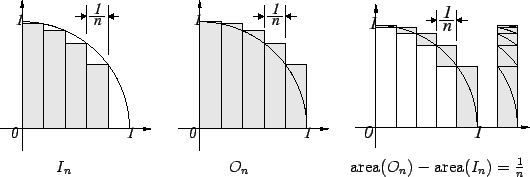
In this example, both of the sets
![]() and
and ![]() are composed of a finite number of rectangles
of width
are composed of a finite number of rectangles
of width
![]() , and from the equation of the circle we can
calculate the heights of the rectangles, and hence we can find
the areas of
, and from the equation of the circle we can
calculate the heights of the rectangles, and hence we can find
the areas of ![]() and
and ![]() . From the third figure
we see that area
. From the third figure
we see that area![]() area
area
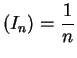 . Hence
if
. Hence
if ![]() , then either
of the numbers area
, then either
of the numbers area![]() or area
or area![]() will give the
area of the quarter-circle with an error of no more than
will give the
area of the quarter-circle with an error of no more than ![]() .
This calculation will involve taking many square roots, so you probably
would not want to carry it out by hand, but with the help of
a computer you could easily find the area of the circle
to five decimals accuracy.
However no amount of computing power would allow you to get
thirty decimals of accuracy from this method in a lifetime, and we will
need to develop some theory to get better approximations.
.
This calculation will involve taking many square roots, so you probably
would not want to carry it out by hand, but with the help of
a computer you could easily find the area of the circle
to five decimals accuracy.
However no amount of computing power would allow you to get
thirty decimals of accuracy from this method in a lifetime, and we will
need to develop some theory to get better approximations.
In some cases we can find exact areas. For example, we will show that
the area of
one arch of a sine curve is ![]() , and the area bounded by the
parabola
, and the area bounded by the
parabola ![]() and the line
and the line ![]() is
is
![]() .
.
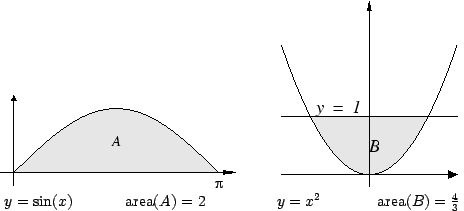
However in other cases the areas are not simply expressible
in terms of known numbers. In these cases we define certain numbers
in terms of areas, for example we will define
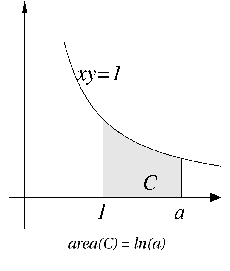
Often we consider general classes of figures, in which case we want
to find a simple formula giving areas
for all of the figures in the class.
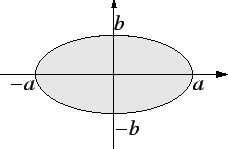
For example we will express the area of the ellipse bounded by the curve
whose equation is
The mathematical tools that we develop for calculating areas,
(i.e. the theory of integration) have many applications
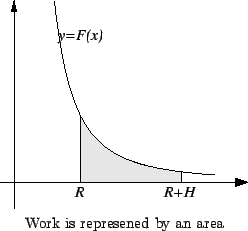
that seem to have little to do with area. Consider a moving object
that is acted upon by a known force ![]() that depends
on the position
that depends
on the position ![]() of the object. (For example, a rocket
propelled upward from the surface of the moon is acted upon
by the moon's gravitational attraction, which is given by
of the object. (For example, a rocket
propelled upward from the surface of the moon is acted upon
by the moon's gravitational attraction, which is given by
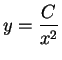 , where
, where
Some of the ideas used in the theory of integration are
thousands of years old. Quite a few
of the technical results in the calculations presented
in these notes
can be found in the writings of Archimedes(287-212 B.C.), although
the way the ideas are presented here is not at all like the
way they are presented by Archimedes.
In the second part of the notes we study the idea of rate of change.
The ideas used in this section began to become common in
early seventeenth century, and they have no counterpart
in Greek mathematics or physics. The problems considered involve
describing motions of moving objects (e.g. cannon balls or planets),
or finding tangents to curves. An important
example of a rate of change is
velocity.
The problem of what is meant by the velocity of a moving
object at a given instant is a delicate one.
At a particular instant of time, the object occupies just one
position in space. Hence during that instant the object does not move.
If it does not move, it is at rest. If it is at rest, then its velocity
must be ![]() (?)
(?)
The ability to find tangents to curves allows us to find maximum
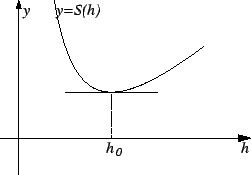
and minimum values of functions. Suppose I want to design a tin can
that holds 1000 cc., and requires a minimum amount of tin. It
is not hard to find a function ![]() such that for each positive
number
such that for each positive
number ![]() ,
the total surface area of a can with height
,
the total surface area of a can with height ![]() and volume
and volume ![]() is equal to
is equal to ![]() .
The graph of
.
The graph of ![]() has the general shape shown in the figure, and
the minimum surface area corresponds to the height
has the general shape shown in the figure, and
the minimum surface area corresponds to the height ![]() shown
in the figure. This value
shown
in the figure. This value ![]() corresponds to the point on the
graph of
corresponds to the point on the
graph of ![]() where the tangent line is horizontal, i.e. where
the slope of the tangent is zero. From the formula for
where the tangent line is horizontal, i.e. where
the slope of the tangent is zero. From the formula for ![]() we will be able to find a formula for the slope of the tangent
to the graph of
we will be able to find a formula for the slope of the tangent
to the graph of ![]() at an arbitrary height
at an arbitrary height ![]() , and to
determine when the slope is zero. Thus we will find
, and to
determine when the slope is zero. Thus we will find ![]() .
.
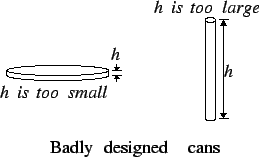
The tool for solving rate problems is the derivative, and the process of calculating derivatives is called differentiation. (There are two systems of notation working here. The term differential was introduced by Gottfried Leibniz(1646-1716) to describe a concept that later developed into what Joseph Louis Lagrange(1736-1813) called the derived function. From Lagrange we get our word derivative, but the older name due to Leibniz is still used to describe the general theory - from which differentials in the sense of Leibniz have been banished.) The idea of derivative (or fluxion or differential) appears in the work of Isaac Newton(1642-1727) and of Leibniz, but can be found in various disguises in the work of a number of earlier mathematicians.
As a rule, it is quite easy to calculate the velocity and acceleration of a moving object, if a formula for the position of the object at an arbitrary time is known. However usually no such formula is obvious. Newton's Second Law states that the acceleration of a moving object is proportional to the sum of the forces acting on the object, divided by the mass of the object. Now often we have a good idea of what the forces acting on an object are, so we know the acceleration. The interesting problems involve calculating velocity and position from acceleration. This is a harder problem than the problem going in the opposite direction, but we will find ways of solving this problem in many cases. The natural statements of many physical laws require the notion of derivative for their statements. According to Salomon Bochner
The mathematical concept of derivative is a master concept, one of the most creative concepts in analysis and also in human cognition altogether. Without it there would be no velocity or acceleration or momentum, no density of mass or electric charge or any other density, no gradient of a potential and hence no concept of potential in any part of physics, no wave equation; no mechanics no physics, no technology, nothing[11, page 276].
At the time that ideas associated with differentiation were being developed,
it was widely recognized that
a logical justification for the subject was completely
lacking. However it was generally agreed that the results of
the calculations based on differentiation
were correct. It took more than a century before
a logical basis for derivatives was developed, and the concepts
of function and real number and limit
and continuity had to be developed before the
foundations could be described. The story is probably not
complete. The modern ``constructions'' of
real numbers based on a general theory of ``sets'' appear to me to
be very vague, and more closely related to philosophy than to
mathematics. However in these notes we will not worry about
the foundations of the real numbers. We will assume that they are
there waiting for us to use,
but we will need to discuss the concepts of function, limit
and continuity in order to get our results.
The fundamental theorem of the calculus says that the
theory of integration, and the theory of differentiation
are very closely related, and that differentiation techniques
can be used for solving integration problems, and vice versa.
The fundamental theorem is usually credited to Newton and
Leibniz independently, but it can be found in various
degrees of generality in a number of earlier writers. It
was an idea floating in the air, waiting to be discovered
at the close of the seventeenth century.