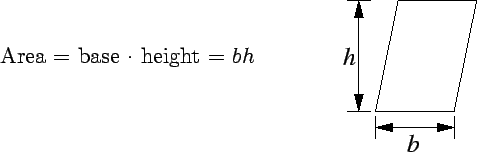
It will be assumed that you are familiar with the results from Euclidean and coordinate geometry listed below.
| (C.110) |
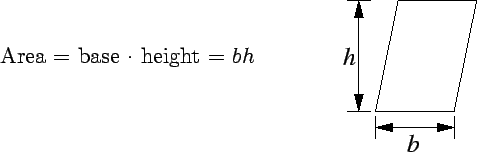
| (C.111) |
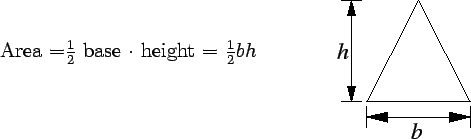
| (C.112) |
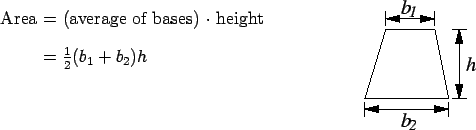
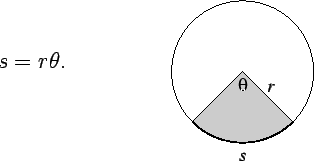
We will always assume that angles are measured in
radians unless otherwise
specified. If an angle ![]() is inscribed in a circle of radius
is inscribed in a circle of radius ![]() and
and ![]() is the length of the subtended arc, then
is the length of the subtended arc, then
A right angle is ![]() and the sum of the angles of a
triangle is
and the sum of the angles of a
triangle is ![]() . When
. When ![]() is four right angles in (C.113)
we get
is four right angles in (C.113)
we get
| (C.114) |
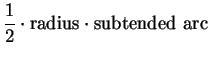 |
|||
 |
|||
| (C.115) |
| (C.116) |