
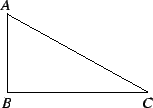
The Pythagorean Theorem: If ![]() is a right triangle with the right angle at
is a right triangle with the right angle at ![]() , then
, then
| (C.117) |
In a given circle, equal arcs subtend equal chords.
A regular hexagon inscribed in a circle has each of its sides equal to the radius of the circle. The radii joining the vertices of this hexagon to the center of the circle decompose the hexagon into six equilateral triangles.

It is assumed that you are familiar with the process of
representing points in the plane by pairs of numbers.
If
![]() and
and
![]() are points
with
are points
with ![]() , then the slope of the segment
joining
, then the slope of the segment
joining ![]() to
to ![]() is defined to be
is defined to be
| (C.118) |
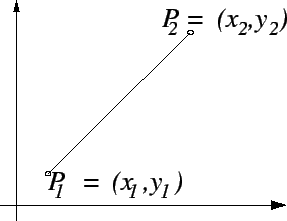
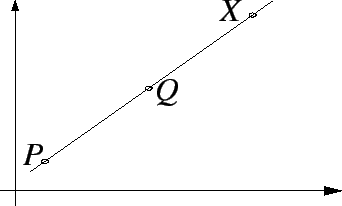
If ![]() we say that
we say that ![]() has undefined slope, or that
has undefined slope, or that
![]() is a vertical segment.
If slope
is a vertical segment.
If slope![]() is zero
we say that
is zero
we say that ![]() is a horizontal segment.
is a horizontal segment.
Let ![]() and
and ![]() be two distinct points in the plane.
If
be two distinct points in the plane.
If ![]() , then the line passing through
, then the line passing through ![]() and
and ![]() is
defined to be the set
of all points of the form
is
defined to be the set
of all points of the form ![]() , where
, where ![]() can be an arbitrary real
number. If
can be an arbitrary real
number. If ![]() , then the line joining
, then the line joining ![]() to
to ![]() is defined to be
the set consisting of
is defined to be
the set consisting of ![]() together with all points
together with all points ![]() such that slope(
such that slope(![]() ) = slope(
) = slope(![]() ). Thus if
). Thus if ![]() then
then ![]() is on the line joining
is on the line joining
![]() to
to ![]() if and only if
if and only if
| (C.121) |
Two lines are parallel, (i.e. they do not intersect or they are identical,) if and only if they both have the same slope or they both have undefined slopes.