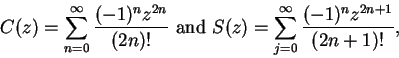Next: 12.4 The Exponential Function
Up: 12. Power Series
Previous: 12.2 Radius of Convergence
Index
If
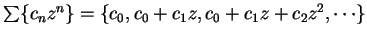 is a power series, then
the series obtained by differentiating the terms of
is a power series, then
the series obtained by differentiating the terms of
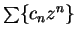 is
is
This is not a power series, but its translate
is.
12.15
Definition (Formal derivative.)
If
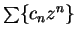
is a power series, then the
formal derivative of
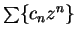
is
I will sometimes write
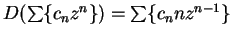
when I think this will
cause no confusion.
Our fundamental theorem on power series is:
12.17
Theorem (Differentiation theorem.)
Let
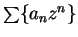 be a power series. Then
be a power series. Then
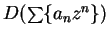 and
and
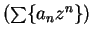 have the same radius of convergence. The function
have the same radius of convergence. The function  associated
with
associated
with
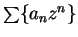 is differentiable in the disc of convergence, and the function
represented by
is differentiable in the disc of convergence, and the function
represented by
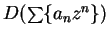 agrees with
agrees with 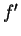 on the disc of convergence.
on the disc of convergence.
The proof is rather technical, and I will postpone it
until section 12.8. I will derive some consequences of it before
proving it (to convince you that it is worth proving).
12.18
Example.
We know that the geometric series
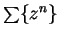
has radius of convergence
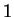
and
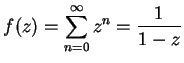
for
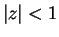
. The differentiation
theorem says
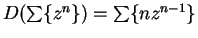
also has radius of convergence
,
and
i.e.,
We can apply the theorem again and get
or
Another differentiation gives us
or
The pattern is clear, and I omit the induction proof that for all
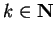
12.19
Exercise.
By assuming the differentiation theorem, we've shown that the series
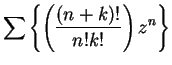
has radius of
convergence
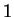
for all
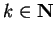
. Verify this directly.
12.20
Exercise.
A
Find formulas for
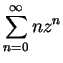
and
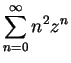
that are valid for
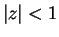
. (You may assume the
differentiation theorem.)
12.21
Example.
By the differentiation theorem, if
then
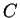
and

are differentiable on

and
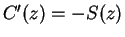
, and
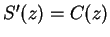
. (We
saw in earlier examples that both series have radius of convergence
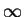
, and
that the formal derivatives satisfy
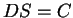
and
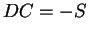
.) Also, clearly
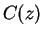
and
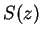
are real when
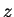
is real. The discussion in example
10.3 then shows
that for real
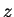
,
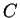
and

agree with the cosine and sine functions you
discussed in your previous calculus course, and in particular that




Next: 12.4 The Exponential Function
Up: 12. Power Series
Previous: 12.2 Radius of Convergence
Index
![]() is a power series, then
the series obtained by differentiating the terms of
is a power series, then
the series obtained by differentiating the terms of
![]() is
is
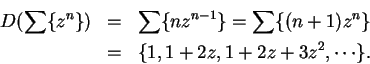
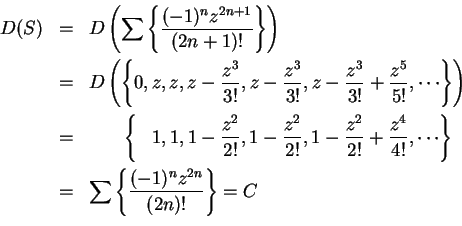
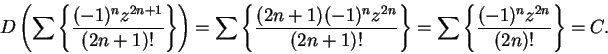
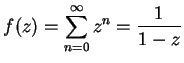 for
for 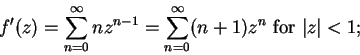
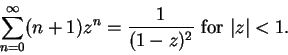
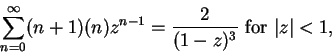
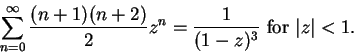
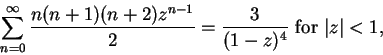
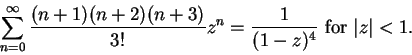
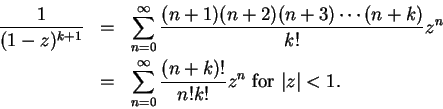
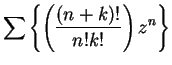 has radius of
convergence
has radius of
convergence 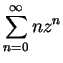 and
and
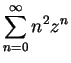 that are valid for
that are valid for