



Next: 12.2 Radius of Convergence
Up: 12. Power Series
Previous: 12. Power Series
Index
12.1
Definition (Power Series.)
Let
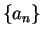
be a sequence of complex numbers. A series of the form
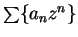
is called a
power series.
We think of a power series as a sequence of polynomials
In general, this sequence will converge for certain complex numbers, and diverge for
other numbers. A power series
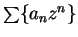
determines a function whose domain
is the set of all
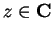
such that
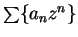
converges.
12.2
Examples.
The geometric series
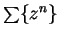
is a power series that converges to
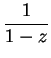
for
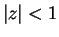
and diverges for
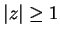
.
The series
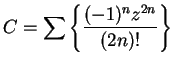 and
and
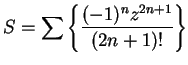 are power series that
converge for all
are power series that
converge for all
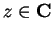 .
. 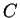 corresponds to the sequence
corresponds to the sequence
and

corresponds to
The limits are
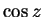
and
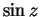
, respectively (by
definition
11.43.)
Every power series
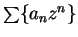 converges at
converges at 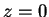 . (The limit is
. (The limit is 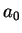 .)
.)
The series 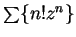 converges only when
converges only when 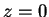 (see exercise 12.5).
(see exercise 12.5).
12.3
Notation (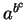 )
)
The expression
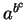
is ambiguous.
Since
and
we see that in general
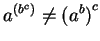
.
We make the convention that
The expression
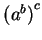
is usually simplified and written
without parentheses by use of exercise
3.64:
12.4
Example.
I would like to consider the series
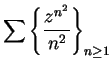
to be a power series. This series corresponds to
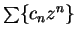
where
which is not identical with
but you should be able to see that one series converges if and only if the other
does, and that they have the same limits. In the future I will sometimes blur the
distinctions between two series like this.
For 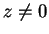 , let
, let
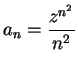 . Then
. Then
If
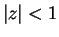
, then
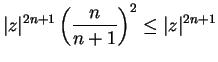
and
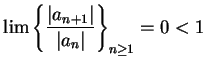
, so by the
ratio test,
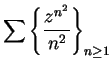
converges
absolutely for
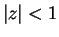
.
If 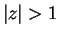 and
and 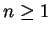 , then
, then
so
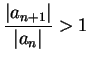
for large
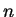
, and the series diverges. If
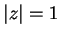
, then
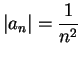
, so
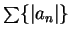
converges by the
comparison test, and
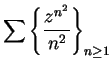
converges absolutely. This shows that the function
is defined for all
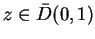
, and determines a function from
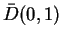
into

.
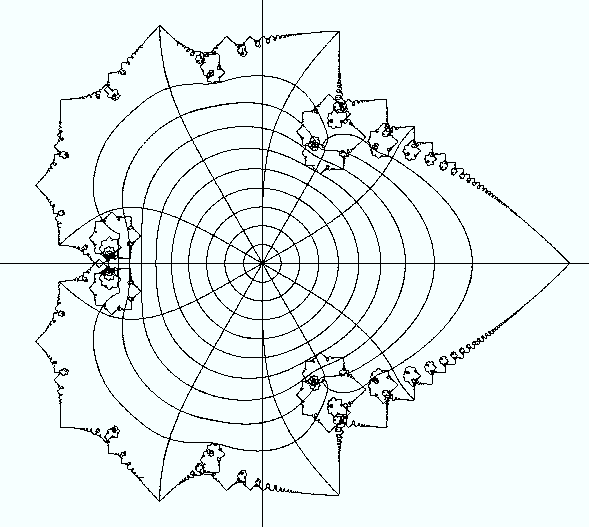
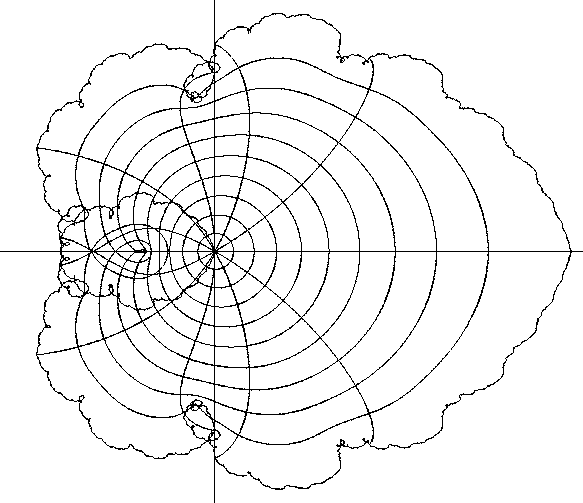
The figure below 12.1
shows the images under  of circles of radius
of circles of radius
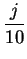 for
for
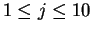 and of rays that divide the disc into twelve
equal parts. The images of the interior circles are nice differentiable curves.
The image of the boundary circle seems to have interesting properties that I do not
know how to demonstrate.
and of rays that divide the disc into twelve
equal parts. The images of the interior circles are nice differentiable curves.
The image of the boundary circle seems to have interesting properties that I do not
know how to demonstrate.
12.5
Exercise.
- a) Show that
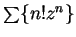 converges only for
converges only for 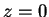 .
.
- b) Show that
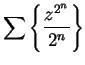 converges if
and only if
converges if
and only if 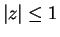 .
.

Image of
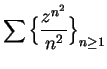
Let
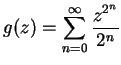 for
for 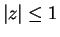 .
.
The figure below 12.1
shows the images under  of circles of radius
of circles of radius
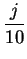 for
for
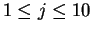 , and of rays that divide the disc into 12 equal parts.
, and of rays that divide the disc into 12 equal parts.
12.6
Exercise.
A
Let
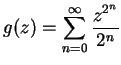
for
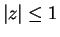
. It appears from figure below
12.1
that
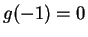
, and
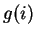
is pure
imaginary. Show that this is the case.
Image of
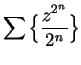
12.7
Entertainment.
It appears from the image of
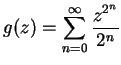
that if
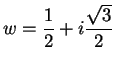
(a cube root of
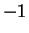
), then
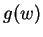
is pure imaginary, and has length a little larger than the length of
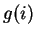
. Show
that this is the case. (From the fact that
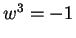
, notice that




Next: 12.2 Radius of Convergence
Up: 12. Power Series
Previous: 12. Power Series
Index
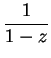 for
for 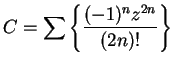 and
and
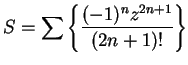 are power series that
converge for all
are power series that
converge for all
![]() .
. ![]() corresponds to the sequence
corresponds to the sequence
![]() converges at
converges at ![]() . (The limit is
. (The limit is ![]() .)
.)
![]() converges only when
converges only when ![]() (see exercise 12.5).
(see exercise 12.5).
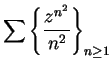 to be a power series. This series corresponds to
to be a power series. This series corresponds to
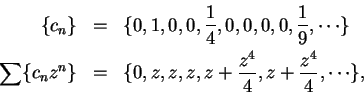
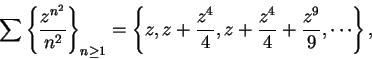
![]() , let
, let
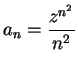 . Then
. Then
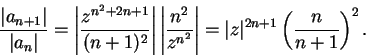
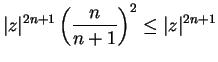 and
and
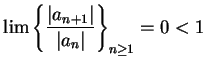 , so by the
ratio test,
, so by the
ratio test,
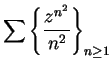 converges
absolutely for
converges
absolutely for ![]() and
and ![]() , then
, then
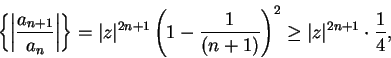
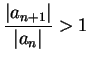 for large
for large 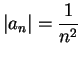 , so
, so 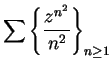 converges absolutely. This shows that the function
converges absolutely. This shows that the function
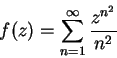
![]() of circles of radius
of circles of radius
![]() for
for
![]() and of rays that divide the disc into twelve
equal parts. The images of the interior circles are nice differentiable curves.
The image of the boundary circle seems to have interesting properties that I do not
know how to demonstrate.
and of rays that divide the disc into twelve
equal parts. The images of the interior circles are nice differentiable curves.
The image of the boundary circle seems to have interesting properties that I do not
know how to demonstrate.
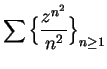
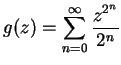 for
for ![]() .
.
![]() of circles of radius
of circles of radius
![]() for
for
![]() , and of rays that divide the disc into 12 equal parts.
, and of rays that divide the disc into 12 equal parts.
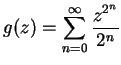 for
for
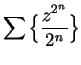
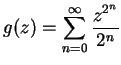 that if
that if
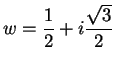 (a cube root of
(a cube root of