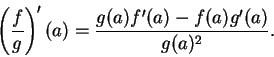Next: 10.2 Differentiable Functions on
Up: 10. The Derivative
Previous: 10. The Derivative
Index
You are familiar with derivatives of functions from
 to
to
 , and with the
motivation of the definition of derivative as the slope of the tangent to a curve.
For complex functions, the geometrical motivation is missing, but the definition is
formally the same as the definition for derivatives of real functions.
, and with the
motivation of the definition of derivative as the slope of the tangent to a curve.
For complex functions, the geometrical motivation is missing, but the definition is
formally the same as the definition for derivatives of real functions.
10.1
Definition (Derivative.)
Let

be a complex valued function with
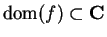
, let

be a point
such that
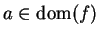
, and

is a limit point of
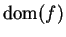
. We say

is
differentiable at 
if the limit
exists. In this case, we denote this limit by
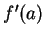
and call
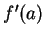
the
derivative of  at
at 
.
By the definition of limit, we can say that  is differentiable at
is differentiable at  if
if
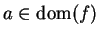 , and
, and  is a limit point of
is a limit point of
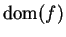 and there exists
a function
and there exists
a function
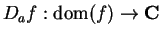 such
that
such
that 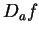 is continuous at
is continuous at  , and
such that
, and
such that
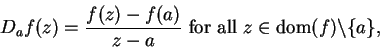 |
(10.2) |
and in this case 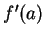 is equal to
is equal to 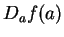 .
.
It is sometimes useful to rephrase condition (10.2) as follows:
 is
differentiable at
is
differentiable at  if
if
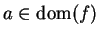 ,
,  is a limit point of
is a limit point of
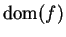 ,
and there is a function
,
and there is a function
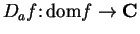 such that
such that 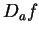 is continuous at
is continuous at  , and
, and
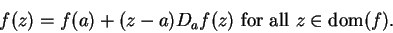 |
(10.3) |
In this case, 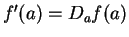 .
.
10.4
Remark.
It follows immediately from (
10.3) that if

is differentiable at

,
then

is continuous at

.
10.5
Example.
Let
be given by
and let
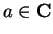
. Then for all
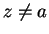
,
If we define
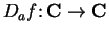
by
then
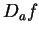
is continuous at

, so

is differentiable at

and
We could also write
this calculation as
Hence

is differentiable at

and
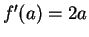
for all
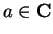
.
10.6
Example.
Let
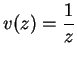
for
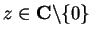
and let
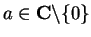
. Then for all
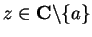
Let
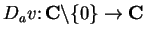
be defined by
Then
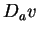
is continuous at

, so
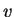
is differentiable at

, and
for all
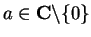
.
10.7
Warning.
The function
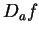
should not be confused with
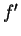
. In the example above
Also it is not good form to say
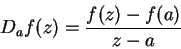 |
(10.8) |
without specifying the condition `` for
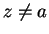
," since someone reading
(
10.8) would assume
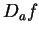
is undefined at

.
10.9
Example.
Let
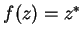
for all
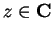
, and let
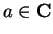
. Let
I claim that
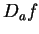
does not have a limit at

,
and hence

is a
nowhere differentiable function.
Let
Then
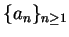
and
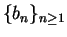
are sequences in
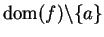
both of which converge
to

. For all
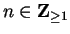
,
so
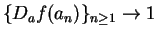
and
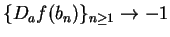
, and hence
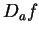
does not have a limit at

.
10.11
Theorem (Sum theorem for differentiable functions.)Let 
be complex
functions, and suppose  and
and  are differentiable at
are differentiable at
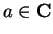 . Suppose
. Suppose  is a limit point of
is a limit point of
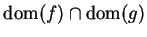 . Then
. Then 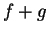 is
differentiable at
is
differentiable at  and
and
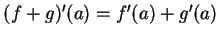 .
.
Proof: Since  are differentiable at
are differentiable at  , there are functions
, there are functions
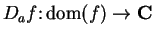 ,
,
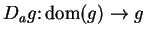 such that
such that 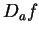 ,
,
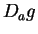 are continuous at
are continuous at  , and
, and
It follows that
and 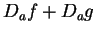 is continuous at
is continuous at  .
.
We can let
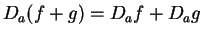 and we see
and we see 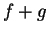 is differentiable at
is differentiable at
 and
and
10.12
Theorem.
Let  be a complex function and let
be a complex function and let
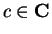 . If
. If  is differentiable at
is differentiable at  ,
then
,
then 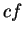 is differentiable at
is differentiable at  and
and
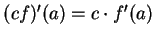 .
.
Proof: The proof is left to you.

Proof: From our hypotheses, there exist functions
such that 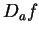 is continuous at
is continuous at  ,
, 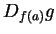 is continuous at
is continuous at 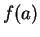 and
and
If
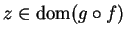 , then
, then
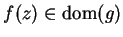 , so we can replace
, so we can replace 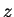 in
(10.15) by
in
(10.15) by 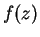 to get
to get
Using (10.14) to rewrite 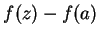 , we get
, we get
Hence we have
and 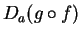 is continuous at
is continuous at  . Hence
. Hence 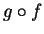 is differentiable
at
is differentiable
at  and
and
10.16
Theorem (Reciprocal rule.)
Let  be a complex function, and let
be a complex function, and let
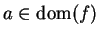 . If
. If  is differentiable at
is differentiable at
 and
and 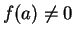 , then
, then
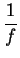 is differentiable at
is differentiable at  and
and
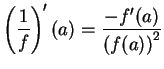 .
.
Proof: If
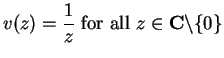 , we saw above that
, we saw above that 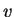 is
differentiable and
is
differentiable and
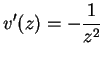 . Let
. Let  be a complex function, and
let
be a complex function, and
let
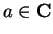 . Suppose
. Suppose  is differentiable at
is differentiable at  , and
, and 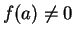 . Then
. Then
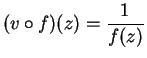 . By the chain rule
. By the chain rule 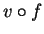 is differentiable
at
is differentiable
at  , and
, and
10.17
Exercise (Product rule.)
A
Let

be complex
functions. Suppose

and

are both
differentiable at

, and that

is a limit point of
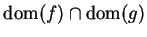
.
Show that
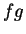
is differentiable at

, and that
10.18
Exercise (Power rule.)
Let

be a complex function, and suppose that

is differentiable at
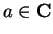
.
Show that
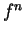
is differentiable at

for all
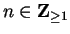
and
(Use induction.)
10.19
Exercise (Power rule.)
A
Let

be a complex function.
suppose that

is differentiable at
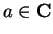
, and
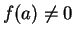
.
Show that
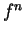
is differentiable at

for all
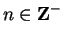
, and
that
for all
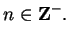
10.20
Exercise (Quotient rule.)
A
Let

be
complex functions and let
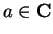
. Suppose

and

are differentiable at

and
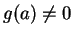
, and

is a limit point of
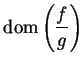
. Show that
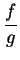
is
differentiable at

and




Next: 10.2 Differentiable Functions on
Up: 10. The Derivative
Previous: 10. The Derivative
Index
![]() to
to
![]() , and with the
motivation of the definition of derivative as the slope of the tangent to a curve.
For complex functions, the geometrical motivation is missing, but the definition is
formally the same as the definition for derivatives of real functions.
, and with the
motivation of the definition of derivative as the slope of the tangent to a curve.
For complex functions, the geometrical motivation is missing, but the definition is
formally the same as the definition for derivatives of real functions.
![]() is differentiable at
is differentiable at ![]() if
if
![]() , and
, and ![]() is a limit point of
is a limit point of
![]() and there exists
a function
and there exists
a function
![]() such
that
such
that ![]() is continuous at
is continuous at ![]() , and
such that
, and
such that
![]() is
differentiable at
is
differentiable at ![]() if
if
![]() ,
, ![]() is a limit point of
is a limit point of
![]() ,
and there is a function
,
and there is a function
![]() such that
such that ![]() is continuous at
is continuous at ![]() , and
, and
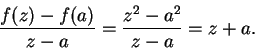
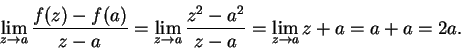
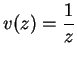 for
for
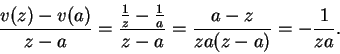
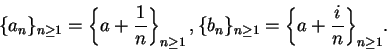
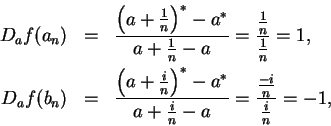
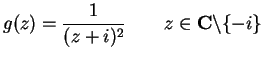 .
.
![]() are differentiable at
are differentiable at ![]() , there are functions
, there are functions
![]() ,
,
![]() such that
such that ![]() ,
,
![]() are continuous at
are continuous at ![]() , and
, and
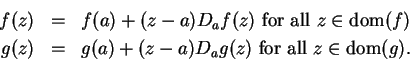
![]() and we see
and we see ![]() is differentiable at
is differentiable at
![]() and
and
![]()
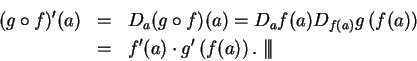
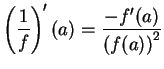 .
.
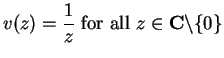 , we saw above that
, we saw above that ![]() is
differentiable and
is
differentiable and
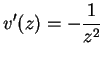 . Let
. Let ![]() be a complex function, and
let
be a complex function, and
let
![]() . Suppose
. Suppose ![]() is differentiable at
is differentiable at ![]() , and
, and ![]() . Then
. Then
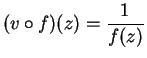 . By the chain rule
. By the chain rule ![]() is differentiable
at
is differentiable
at ![]() , and
, and
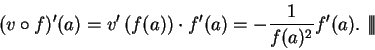
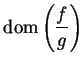 . Show that
. Show that