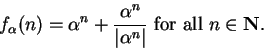8.1
Definition (Composition)
Let
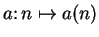
be a complex sequence. Let
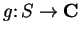
be a
function such that
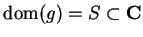
, and
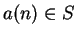
for all

. Then the
composition 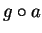
is
the sequence such that
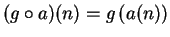
for all

. If

is a sequence, I will often
write
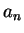
instead of
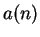
. Then
8.2
Examples.
If
and
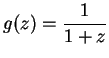
for all
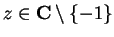
,
then
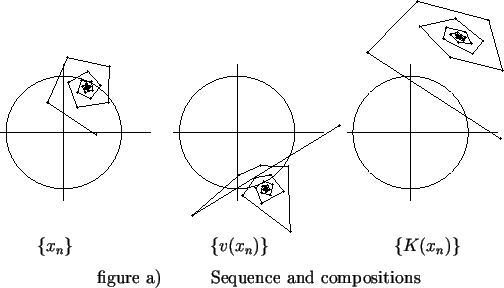
Figure a) below shows representations of 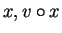 and
and 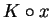 where
where
I leave it to you to check that
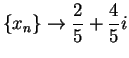
, and
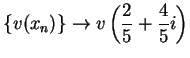
, and
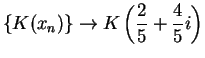
.
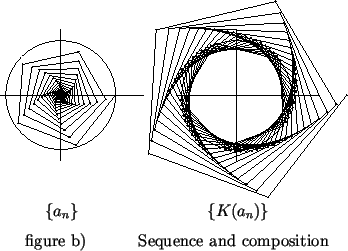
Figure b) shows representations for

and
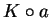
where
and
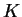
is defined as in (
8.3). Here it is easy to check that
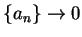
. From the figure,
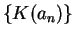
doesn't appear to converge.
8.4
Exercise.
A
Let
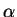
be a
non-zero complex number with
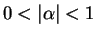
.
Let
Under what conditions on
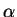
does
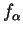
converge? What does it converge
to? (Your answer should show that the sequence
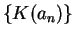
from the previous
example does not converge.)
8.5
Definition (Complex function.)
By a
complex function I will mean a function whose domain is a subset of

,
and whose codomain is

. I will consider functions from

to

to be
complex functions by identifying a function
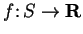
with a function
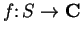
in the expected manner.
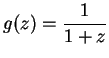 for all
for all
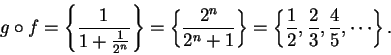
![]() and
and ![]() where
where
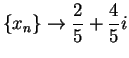 , and
, and
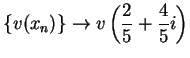 , and
, and
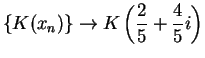 .
Figure b) shows representations for
.
Figure b) shows representations for