


Next: Index
Up: Numbers
Previous: A. Hints and Answers
Index
B. Associativity and Distributivity of Operations in
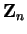
Let
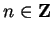 satisfy
satisfy 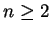 . Let
. Let
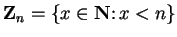 . Let
. Let 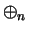 and
and 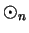 be the binary operations on
be the binary operations on
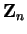 defined by
defined by
Thus for all
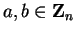 ,
,
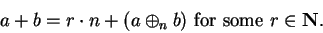 |
(B.1) |
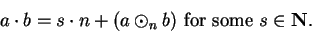 |
(B.2) |
We will show that 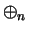 and
and 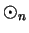 are associative by using the usual
properties of addition and multiplication on
are associative by using the usual
properties of addition and multiplication on
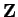 .
.
B.3
Lemma.
Let
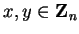 ,
,
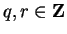 . If
. If 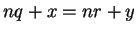 , then
, then 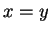 and
and 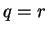 .
.
Proof:
- Case 1. Suppose
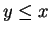 . Then by our assumptions,
. Then by our assumptions,
and
So
Since 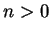 , it follows that
, it follows that 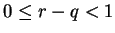 and since
and since 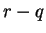 is an integer
is an integer 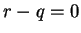 , so
, so
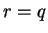 . Then
. Then 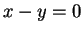 , so
, so 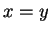 .
.
- Case 2. If
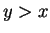 , use Case 1 with
, use Case 1 with 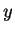 and
and 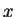 interchanged.
interchanged.
B.4
Theorem.
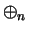 is associative on
is associative on
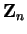 .
.
Proof: Let
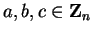 . Then
. Then
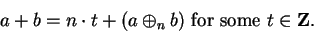 |
(B.5) |
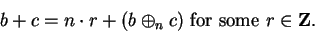 |
(B.6) |
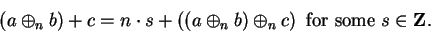 |
(B.7) |
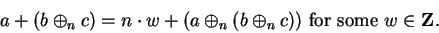 |
(B.8) |
By adding 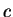 to both sides of (B.5), we get
to both sides of (B.5), we get
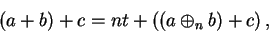 |
(B.9) |
and by adding 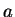 to both sides of (B.6), we get
to both sides of (B.6), we get
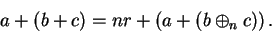 |
(B.10) |
Replace
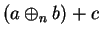 in (B.9) by its value from (B.7) to get
in (B.9) by its value from (B.7) to get
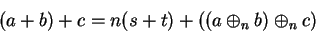 |
(B.11) |
and replace
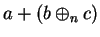 in (B.10) by its value from (B.8) to
get
in (B.10) by its value from (B.8) to
get
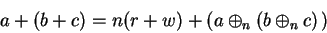 |
(B.12) |
By (B.11) and (B.12) and the associative law in
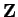 ,
,
the associativity of 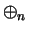 follows from lemma (B.3).
follows from lemma (B.3).
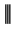
B.13
Theorem.
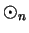 is associative on
is associative on
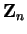 .
.
Proof: The proof is nearly identical with the proof that 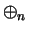 is associative.
is associative.
B.14
Theorem.
The distributive law holds in
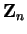 ; i.e., for all
; i.e., for all
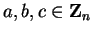 ,
,
Proof: We have
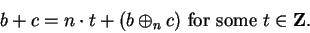 |
(B.15) |
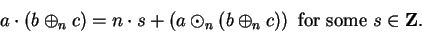 |
(B.16) |
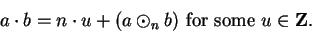 |
(B.17) |
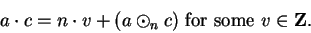 |
(B.18) |
Multiply both sides of (B.15) by 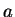 to get
to get
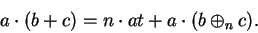 |
(B.19) |
Replace
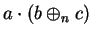 in (B.19) by its value from (B.16) to get
in (B.19) by its value from (B.16) to get
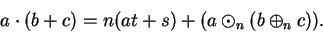 |
(B.20) |
Now add equations (B.17) and (B.18) to get
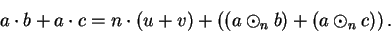 |
(B.21) |
We know that for some
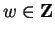 ,
,
and if we substitute this into (B.21), we obtain
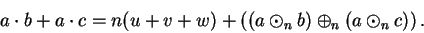 |
(B.22) |
From (B.20) and (B.22) and the distributive law in
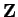 , we conclude
, we conclude
The distributive law follows from lemma B.3.



Next: Index
Up: Numbers
Previous: A. Hints and Answers
Index
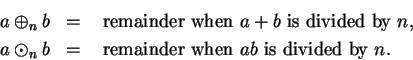
![]() . Then
. Then
![]() is associative.
is associative.