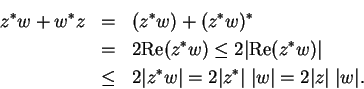6.1 Absolute Value and Complex Conjugate

6.1   Definition (Complex Numbers, $\mbox{{\bf C}}$.) We denote the complexification of $\mbox{{\bf R}}$ by $\mbox{{\bf C}}$, and we call $\mbox{{\bf C}}$ the complex numbers.

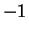
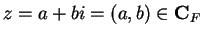
6.2   Definition (Absolute value.) In exercise 4.23A we showed that (for any field $F$ in which $-1$ is not a square), if $z=a+bi=(a,b)\in\mbox{{\bf C}}_F$, then

$$z^*z=a^2+b^2\in F.$$

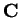
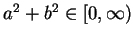
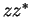
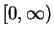
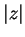
If we are working in $\mbox{{\bf C}}$, then $a^2+b^2\in[0,\infty)$ and hence $zz^*$ has a unique square root in $[0,\infty)$, which we denote by $\vert z\vert$ and call the absolute value of $z$.

$$\vert z\vert=(z^*z)^{1/2} \mbox{ for all } z\in\mbox{{\bf C}}.$$

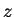
We note that

$$\begin{eqnarray*} &\;&\vert z\vert\in\mbox{${\mbox{{\bf R}}}^{+}$}\cup\{0\} \mbo... ...\;&\vert z\vert=0\hspace{1ex}\Longleftrightarrow\hspace{1ex}z=0. \end{eqnarray*}$$

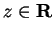
Also note that for $z\in\mbox{{\bf R}}$, this definition agrees with our old definition of absolute value in $\mbox{{\bf R}}$.

6.3   Definition (Real and imaginary parts.) Let $z\in\mbox{{\bf C}}$ and write $z=x+iy$ where $x,y\in\mbox{{\bf R}}$. We call $x$ the real part of $z$, and we call $y$ the imaginary part of $z$ (note that the imaginary part of $z$ is real), and we write

$$x=\mbox{\rm Re}(z),\;\; y=\mbox{\rm Im}(z) \mbox{ if } z=(x,y)=x+iy.$$

6.4   Theorem. Let $z,w$ be complex numbers. Then

a)

$\vert zw\vert=\vert z\vert \; \vert w\vert$.

b)

$${ \left\vert {z\over w}\right\vert ={{\vert z\vert}\over {\vert w\vert}}}$$ if $w\neq 0$.

c)

$${ \mbox{\rm Re}(z)={{z+z^*}\over 2}}$$.

d)

$${ \mbox{\rm Im}(z)={{z-z^*}\over {2i}}}$$.

e)

$\vert\mbox{\rm Re}(z)\vert\leq \vert z\vert$.

f)

$\vert\mbox{\rm Im}(z)\vert\leq \vert z\vert$.

g)

$\vert z^*\vert=\vert z\vert$.

h)

$\mbox{\rm Re}(z+w)=\mbox{\rm Re}(z)+\mbox{\rm Re}(w)$.

i)

$\mbox{\rm Im}(z+w)=\mbox{\rm Im}(z)+\mbox{\rm Im}(w)$.

Proof: By using properties of the complex conjugate proved in exercise 4.23A, we have

$$\vert zw\vert^2=(zw)^*(zw)=z^*w^*zw=z^*zw^*w=\vert z\vert^2 \vert w\vert^2.$$

Hence by uniqueness of square roots, $\vert zw\vert=\vert z\vert \; \vert w\vert$. The proofs of b), c), d), e), f), g), h) and i) are left to you. $\mid\!\mid\!\mid$

6.5   Exercise. Prove parts b), c), d), e), f), g), h) and i) of Theorem 6.4. A

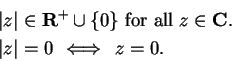
6.6   Theorem (Triangle inequality.) Let $z,w\in\mbox{{\bf C}}$. Then

$$\vert z+w\vert\leq\vert z\vert+\vert w\vert.$$

Proof: For all $z,w\in\mbox{{\bf C}}$,

$$\vert z+w\vert^2 = (z+w)^*\cdot(z+w)=(z^*+w^*)\cdot(z+w)$$

$$= z^*z+z^*w+w^*z+w^*w$$

$$= \vert z\vert^2+z^*w+w^*z+\vert w\vert^2.$$ (6.7)

Now since $z^{**} =z$, we have

$$\begin{eqnarray*} z^*w+w^*z&=&(z^*w)+(z^*w)^* \\ &=&2\mbox{\rm Re}(z^*w)\leq 2\... ...\vert=2\vert z^*\vert\;\vert w\vert=2\vert z\vert\;\vert w\vert. \end{eqnarray*}$$

Hence, from (6.7),

$$\vert z+w\vert^2\leq\vert z\vert^2+2\vert z\vert\;\vert w\vert+\vert w\vert^2=(\vert z\vert+\vert w\vert)^2,$$

and it follows that

$$\vert z+w\vert\leq \vert z\vert+\vert w\vert.\mbox{ $\mid\!\mid\!\mid$}$$