



Next: 4.2 Complex Conjugate.
Up: 4. The Complexification of
Previous: 4. The Complexification of
Index
Throughout this chapter,  will represent a field in which
will represent a field in which 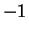 is not a square.
For example, in an ordered field
is not a square.
For example, in an ordered field 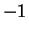 is not a square, but in
is not a square, but in
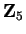 ,
, 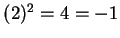 so
so 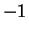 is a square. In
is a square. In
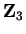 ,
,
so 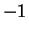 is not a square in
is not a square in
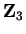 .
.
Let  be a field in which
be a field in which 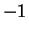 is not a square. I am going to construct a new
field
is not a square. I am going to construct a new
field
 which contains (a copy of)
which contains (a copy of)  and a new element
and a new element 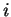 such that
such that
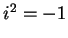 . The elements of
. The elements of
 will all have the form
will all have the form
where  and
and 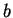 are in
are in  . I'll call
. I'll call
 the complexification
of
the complexification
of  .
Before I start my construction, note that if
.
Before I start my construction, note that if 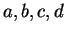 are in
are in  and
and 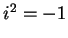 , then
by the usual field axioms
, then
by the usual field axioms
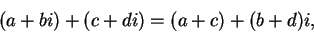 |
(4.1) |
and
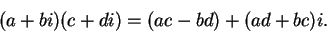 |
(4.2) |
Let  be a field in which
be a field in which 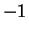 is not a square. Let
is not a square. Let
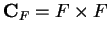 denote the
Cartesian product of
denote the
Cartesian product of  with itself (Cf. definition 1.55). I define two binary
operations
with itself (Cf. definition 1.55). I define two binary
operations 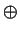 and
and 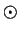
 as follows (cf. (4.1) and
(4.2)): for all
as follows (cf. (4.1) and
(4.2)): for all
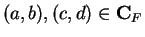 ,
,
and
We will now show that
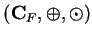 is a field.
is a field.
4.3
Theorem (Associativity of 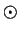 .)
The operation
.)
The operation 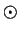 is associative on
is associative on
 .
.
Proof: Let 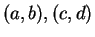 and
and 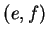 be elements in
be elements in
 . Then
. Then
Also,
Now by using the field properties of  , we see that the (4.4) and
(4.5) are equal, and hence
, we see that the (4.4) and
(4.5) are equal, and hence
Hence, 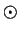 is associative on
is associative on
 .
.

I expect the multiplicative identity for
 to be
to be 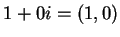 .
.
4.6
Theorem (Multiplicative identity for
 .)The element
.)The element 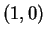 is an identity for
is an identity for  on
on
 .
.
Proof: For all
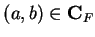 , we have
, we have
and
4.7
Exercise.
- a)
- Show that
 is associative on
is associative on
 .
.
- b)
- Show that there is an identity for
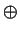 on
on
 .
.
- c)
- Show that every element in
 has an inverse for
has an inverse for 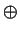 .
.
- d)
- Show that
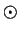 is commutative on
is commutative on
 .
.
- e)
- Show that the distributive law holds for
 .
.
- f)
- Show that the additive and multiplicative identities for
 are
different.
are
different.
As a result of exercise 4.7 and the two previous theorems, we have verified
that
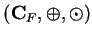 satisfies all of the field axioms except existence of
multiplicative inverses. Note that up to this point we have never used the
assumption that
satisfies all of the field axioms except existence of
multiplicative inverses. Note that up to this point we have never used the
assumption that 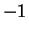 is not a square in
is not a square in  .
.
4.8
Theorem (Existence of multiplicative inverses.)Let  be a field in which
be a field in which 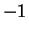 is not a square and let
is not a square and let 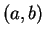 be an element in
be an element in
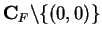 . Then
. Then 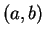 has an inverse for
has an inverse for  .
.
Proof: Let
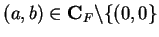 . I want to find a point
. I want to find a point
 such that
such that
Since multiplication is commutative, this shows that
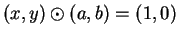 and
hence that
and
hence that 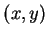 is a multiplicative inverse for
is a multiplicative inverse for 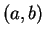 . I want
. I want
so I want
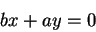 |
(4.9) |
and
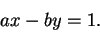 |
(4.10) |
Multiply the first equation by 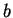 and the second by
and the second by  to get
to get
If we add these equations, we get
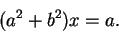 |
(4.11) |
In the next lemma I'll show that if 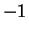 is not a square then
is not a square then 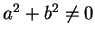 for all
for all
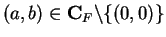 , so by (4.11),
, so by (4.11),
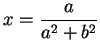 .
Now multiply (4.9) by
.
Now multiply (4.9) by  and (4.10) by
and (4.10) by 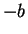 to get
to get
If we add these equations, we get
so
I've shown that if
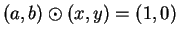 , then
, then
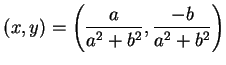 . A direct calculation shows that this
works:
. A direct calculation shows that this
works:
4.12
Remark.
The above proof shows that for all
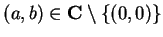
,
4.13
Lemma.
Let  be a field in which
be a field in which 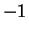 is not a square. Let
is not a square. Let
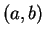 be an element in
be an element in
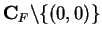 . Then
. Then 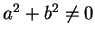 .
.
Proof: Since
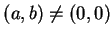 , either
, either 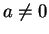 or
or 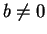 .
.
- Case 1:
- Suppose
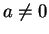 , then
, then 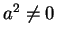 , so
, so
Since 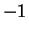 is not a square in
is not a square in  ,
, 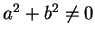 .
.
- Case 2:
- Suppose
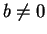 . Repeat the argument of Case 1 with the roles of
. Repeat the argument of Case 1 with the roles of
 and
and 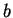 interchanged.
interchanged.

We now have verified all of the field axioms so we know that
 is a field.
Hence we can calculate in
is a field.
Hence we can calculate in
 using all of the algebraic results that have been
proved to hold in all fields.
using all of the algebraic results that have been
proved to hold in all fields.
4.14
Notation (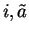 )
)
Let

be a field in which
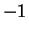
is not a square. We will denote the pair
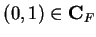
by
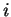
,
and if
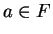
we will denote the pair
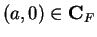
by
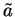
.
We have
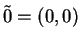 is the additive identity for
is the additive identity for
 , and
, and
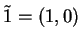 is
the multiplicative identity for
is
the multiplicative identity for
 . If
. If 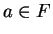 , then
, then
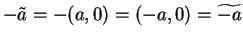 . Also
. Also
so 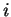 is a square root of
is a square root of 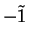 .
.
If 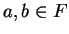 , then
, then
and hence every element
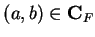 can be written in the form
can be written in the form
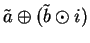 . We have
. We have
Hence
 contains a `` copy of
contains a `` copy of  ".
Each element
".
Each element  in
in  corresponds to
a unique
corresponds to
a unique 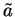 in
in
 in such a way that addition in
in such a way that addition in
 corresponds to
addition in
corresponds to
addition in  and multiplication in
and multiplication in
 corresponds
to multiplication in
corresponds
to multiplication in  . We will
henceforth drop the tildes, and we'll denote
. We will
henceforth drop the tildes, and we'll denote 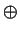 by
by 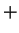 and
and 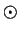 by
by 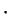 as is usual in fields. Then every element in
as is usual in fields. Then every element in
 can be written uniquely as
can be written uniquely as
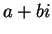 where
where 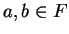 and
and 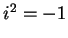 .
.
We consider  to be a subset of
to be a subset of
 . An element
. An element 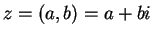 of
of
 is in
is in
 if and only if
if and only if 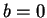 . If
. If 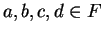 , then
, then
4.15
Examples.
I will find the square roots
of
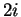
in
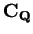
. Let
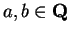
. Then
Now
and
which is impossible. The only possible square roots of
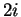
are
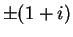
. You
can easily verify that these are square roots of
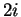
.
4.16
Example.
I can solve the quadratic equation
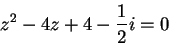 |
(4.17) |
in
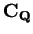
by using the
quadratic formula for
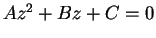
.
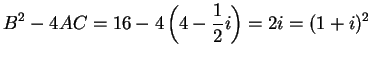
(by the previous example).
Since
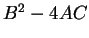
is a square, the equation has the solution set
4.18
Exercise.
Check that
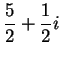
and
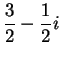
are solutions to (
4.17).
4.20
Entertainment.
We noted earlier that
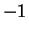
is not a square in
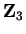
, so
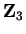
has a
complexification, which is a field with 9 elements. Show that if
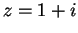
, then the 9
elements in
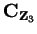
are
Can you figure out before you make any calculations which of these elements is
?




Next: 4.2 Complex Conjugate.
Up: 4. The Complexification of
Previous: 4. The Complexification of
Index
![]() be a field in which
be a field in which ![]() is not a square. I am going to construct a new
field
is not a square. I am going to construct a new
field
![]() which contains (a copy of)
which contains (a copy of) ![]() and a new element
and a new element ![]() such that
such that
![]() . The elements of
. The elements of
![]() will all have the form
will all have the form
![]() be a field in which
be a field in which ![]() is not a square. Let
is not a square. Let
![]() denote the
Cartesian product of
denote the
Cartesian product of ![]() with itself (Cf. definition 1.55). I define two binary
operations
with itself (Cf. definition 1.55). I define two binary
operations ![]() and
and ![]()
![]() as follows (cf. (4.1) and
(4.2)): for all
as follows (cf. (4.1) and
(4.2)): for all
![]() ,
,
![]() and
and ![]() be elements in
be elements in
![]() . Then
. Then
![]() to be
to be ![]() .
.
![]() , we have
, we have
![]() satisfies all of the field axioms except existence of
multiplicative inverses. Note that up to this point we have never used the
assumption that
satisfies all of the field axioms except existence of
multiplicative inverses. Note that up to this point we have never used the
assumption that ![]() is not a square in
is not a square in ![]() .
.
![]() . I want to find a point
. I want to find a point
![]() such that
such that
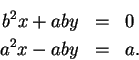
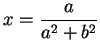 .
Now multiply (4.9) by
.
Now multiply (4.9) by 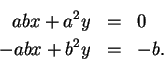
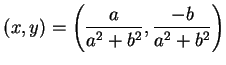 . A direct calculation shows that this
works:
. A direct calculation shows that this
works:
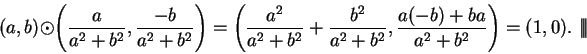
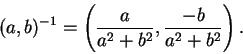
![]() , either
, either ![]() or
or ![]() .
.
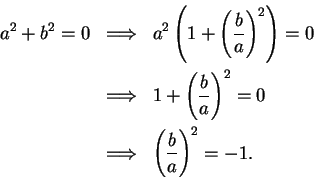
![]() is the additive identity for
is the additive identity for
![]() , and
, and
![]() is
the multiplicative identity for
is
the multiplicative identity for
![]() . If
. If ![]() , then
, then
![]() . Also
. Also
![]() , then
, then
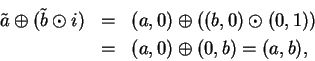
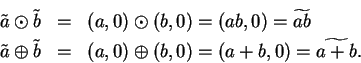
![]() to be a subset of
to be a subset of
![]() . An element
. An element ![]() of
of
![]() is in
is in
![]() if and only if
if and only if ![]() . If
. If ![]() , then
, then
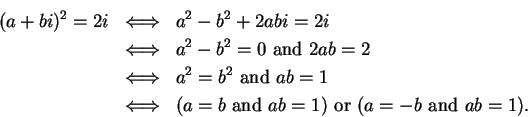
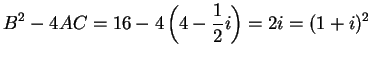 (by the previous example).
Since
(by the previous example).
Since 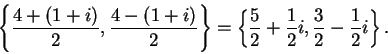
 in the form
in the form