



Next: 3.2 Integers and Rationals.
Up: 3. Induction and Integers
Previous: 3. Induction and Integers
Index
3.1
Definition (Inductive set.)
Let

be a field. A subset
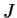
of

is
inductive
if it satisfies the two
conditions:
- i)
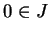 .
.
- ii)
- for all
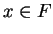 ,
,
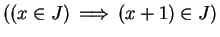 .
.
3.2
Examples.
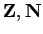
and
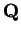
are inductive sets in
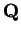
.
Every field
is an inductive subset of itself.
If 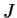 is an inductive subset of
is an inductive subset of  , then
, then
etc. Hence every inductive set contains
If 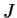 is an inductive subset of
is an inductive subset of
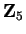 , then
, then
so the only inductive subset of
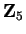
is
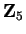
itself. The set
is an inductive subset in
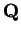
.
3.3
Exercise.
Which of the following subsets of
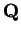
are inductive?
3.4
Exercise.
- a)
- Find an inductive subset
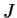 of
of
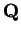 , such that
, such that
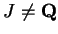 and
and
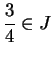 .
.
- b)
- Find an inductive subset
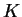 of
of
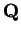 , such that
, such that
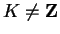 and
and
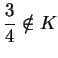 .
.
3.5
Definition (Natural numbers in  .)
.)
Let

be a field, and let
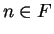
. Then

is a
natural number in 
if

is in every inductive subset of

. The set of all natural numbers in

will
be denoted by

.
3.6
Example.
By the first example in
3.2, for every field

If
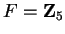 ,
,
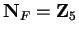 .
.
3.7
Remark.
By the definition of

,

is a subset of every inductive
subset of

, i.e.,
3.8
Theorem.
Let  be a field. Then the set
be a field. Then the set
 of natural numbers in
of natural numbers in  is an inductive
set.
is an inductive
set.
Proof: Since  is in every inductive set,
is in every inductive set,
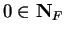 . Let
. Let 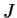 be an inductive
subset of
be an inductive
subset of  . Then for all
. Then for all 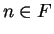 ,
,
Hence
Hence
 is inductive.
is inductive.

3.9
Remark.
We summarize the previous theorem and remark by saying
``

is the
smallest inductive subset of

."

is an inductive set, and it's a subset of
every other inductive set. You should expect that
(whatever ``
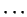
" might mean).
Proof: Let  be a proposition form on
be a proposition form on
 satisfying (3.11) and
(3.12). Let
satisfying (3.11) and
(3.12). Let
I want to show that 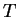 is inductive. Well,
is inductive. Well, 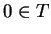 , by (3.11). Let
, by (3.11). Let  be any element in
be any element in  .
.
- Case 1.
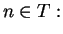
- Case 2.
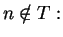
If 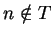 , then
, then 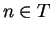 is false, so
is false, so
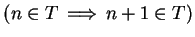 is true.
is true.
Thus
for all 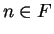 ,
,
This shows that 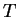 is inductive. Since every inductive set contains
is inductive. Since every inductive set contains
 ,
,
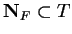 ; i.e., for all
; i.e., for all
 ,
, 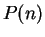 is true.
is true.

3.13
Theorem.
Let  be a field, and let
be a field, and let 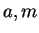 be natural numbers in
be natural numbers in  . Then
. Then 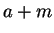 and
and 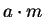 are in
are in
 .
.
Proof: Let  be the proposition form on
be the proposition form on
 defined by
defined by
Then 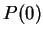 says ``
says ``
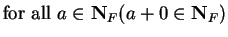 " which is true. For all
" which is true. For all
 ,
,
By the induction theorem, 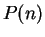 is true for all
is true for all
 ; i.e.,
; i.e.,
Now define a proposition form 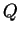 on
on
 by
by
Then 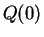 says ``
says ``
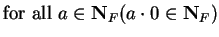 " which is true.
For all
" which is true.
For all
 ,
,
By the induction theorem, 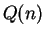 is true for all
is true for all
 ; i.e.,
; i.e.,
3.14
Theorem.
Let  be an ordered field. Then for all
be an ordered field. Then for all
 , we have
, we have
Proof: Define a proposition form  on
on
 by
by
Clearly 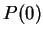 is true. let
is true. let
 . To show that
. To show that
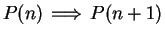 , I'll show that
, I'll show that
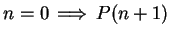 and that
and that
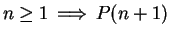 . Well
. Well
and
Hence
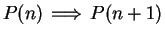 , and by induction
, and by induction 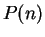 is true for all
is true for all
 .
.

3.15
Corollary.
Let  be an ordered field. Then there is no element
be an ordered field. Then there is no element
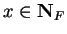 such that
such that
3.16
Lemma.
Let  be an ordered field. Then
be an ordered field. Then
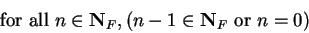 |
(3.17) |
Proof: Define a proposition form  on
on
 by
by
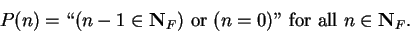 |
(3.18) |
Then 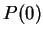 is true. Let
is true. Let
 .
To show that
.
To show that
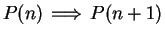 , I'll show
that
, I'll show
that
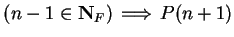 and that (
and that (
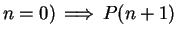 . Well,
. Well,
and
Hence
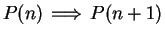 , and by induction,
, and by induction, 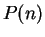 is true for all
is true for all
 .
.

3.19
Theorem.
Let  be an ordered field
and let
be an ordered field
and let
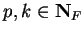 . Then
. Then
Proof: For each
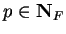 define a proposition form
define a proposition form 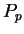 on
on
 by
by
I'll show that for each
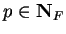 ,
, 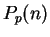 is true for all
is true for all
 .
Now
.
Now 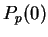 says
``
says
``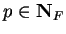 or
or 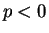 " which is true, since
" which is true, since
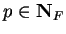 .
Now let
.
Now let
 . To show that
. To show that
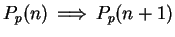 , I'll show that
, I'll show that
and that
By the previous lemma
Also
This completes the proof that
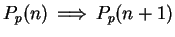 , so by induction
, so by induction 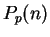 is
true for all
is
true for all
 .
.

3.20
Corollary.
Let  be an ordered field, and let
be an ordered field, and let
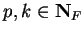 .
If
.
If 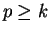 , then
, then
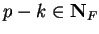 .
.
Proof: Suppose
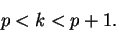 |
(3.22) |
Then
Since 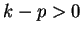 , the previous theorem says
, the previous theorem says
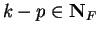 . This contradicts corollary
3.15, so (3.22) is false.
. This contradicts corollary
3.15, so (3.22) is false.

3.23
Theorem (Least Element Principle.)
Let  be an ordered field. Then every non-empty subset
be an ordered field. Then every non-empty subset  of
of
 contains
a least element, i.e. if
contains
a least element, i.e. if
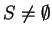 , then there is some element
, then there is some element
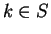 such that
such that 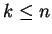 for all
for all 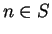 .
.
Proof: I will show that if  is a subset of
is a subset of
 having no least
element, then
having no least
element, then 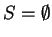 .
.
Let  be a subset of
be a subset of
 having no least element. For each
having no least element. For each
 define
a proposition
define
a proposition 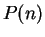 by
by
Now 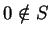 , since if
, since if  were in
were in  it would be a least element for
it would be a least element for
 . Hence all elements in
. Hence all elements in  are greater than
are greater than  , and
, and 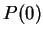 is true.
Now let
is true.
Now let  be a generic element of
be a generic element of
 . Then
. Then
since if 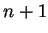 were in
were in  , it would be a least element for
, it would be a least element for  .
Thus
.
Thus
and by induction, 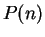 is true for all
is true for all
 .
It follows that
.
It follows that 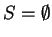 , since if
, since if  contained an element
contained an element  , then
, then
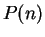 would say that
would say that 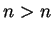 .
.

3.24
Exercise.
A
Let

be an ordered field. Show that
there is a non-empty subset

of
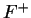
that has no smallest element, i.e.
there is a set
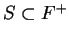
such that
3.25
Example.
Let

be an ordered field. Let

be the proposition form on

defined by
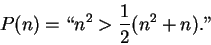 |
(3.26) |
Then for all

Hence
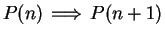
for all

. Now note:
Since
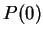
is false, I cannot apply the induction theorem. Notice that when I
prove
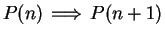
I do
not assume that
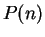
is true. (Although I
might as well, since I know
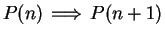
is true if
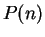
is false.)
Proof: Let 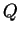 be the proposition form on
be the proposition form on
 defined by
defined by
(observe that
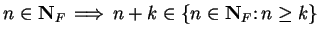 so
so 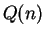 is
defined). Then
is
defined). Then 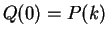 , so
, so 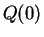 is true by (3.28). For all
is true by (3.28). For all
 ,
,
so
By the induction theorem, 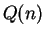 is true for all
is true for all
 ; i.e.,
; i.e., 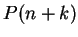 is true
for all
is true
for all
 . To complete the proof, I need to show that
. To complete the proof, I need to show that
It is clear that
To show the opposite inclusion, observe that if
 and
and 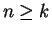 , then
, then
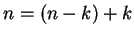 , and by theorem 3.19,
, and by theorem 3.19,
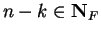 .
.

3.30
Example.
Let

be an ordered field, and let

be the proposition form on

defined by
In example
3.25, we showed that
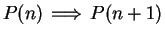
for all

and
that
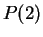
is true. Hence, by our generalized induction theorem we can conclude
that
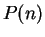
is true for all

with
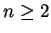
.
3.31
Exercise.
Let

be a field
and let
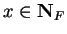
. We say

is
even
if
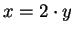
for some
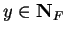
, and we say

is
odd if
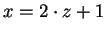
for some
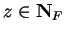
.
- a)
- What are the even numbers in
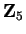 ?
?
- b)
- What are the odd numbers in
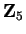 ?
?
3.32
Exercise.
A
- a)
- Let
 be a field. Prove that every element in
be a field. Prove that every element in
 is either even or
odd. HINT: Let
is either even or
odd. HINT: Let 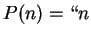 is even or
is even or  is odd".
is odd".
- b)
- Let
 be an ordered field. Prove that
no element of
be an ordered field. Prove that
no element of
 is both even and odd. Why doesn't this contradict the result of exercise
3.31?
is both even and odd. Why doesn't this contradict the result of exercise
3.31?
3.33
Note.
The question of whether to consider

to be a natural number is not
settled. Some authors start the natural numbers at

, other authors start them at
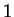
. It is interesting to note that Aristotle did not consider
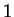
to be a number.
 for ``one" signifies a measure of some plurality, and ``
a number" signifies a measured plurality or a plurality of measures. Therefore, it is
also with good reason that unity is not a number; for neither is a measure measures,
but a measure is a principle, and so is unity
for ``one" signifies a measure of some plurality, and ``
a number" signifies a measured plurality or a plurality of measures. Therefore, it is
also with good reason that unity is not a number; for neither is a measure measures,
but a measure is a principle, and so is unity  .
[5, page 237, N, 1, 1088a5]
.
[5, page 237, N, 1, 1088a5]
Zero was first recognized to be a number around the ninth century. According to
[31, page 185] Mahavira (ninth century)
noted that any number multiplied
by zero produces zero, and any number divided by zero remains unchanged! Bhaskara
(1114-1185) said that a number divided by  is called an infinite quantity.
is called an infinite quantity.
Although arguments that are essentially arguments by induction appear in
Euclid,
the
first clear statement of the induction principle is usually credited to Blaise
Pascal.
(1623-1662) who used induction to prove properties of Pascal's Triangle.[36, page
73]
I believe that the idea of defining the natural numbers to be things that are in
every inductive set should be credited to Giuseppe Peano [37, page 94, Axiom 9]. In.
1889, Peano gave a set of axioms for natural numbers
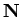 (starting with
(starting with 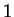 ), one of
which can be paraphrased as: If
), one of
which can be paraphrased as: If 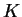 is any set, such that
is any set, such that 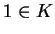 and for all
and for all
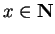 ,
,
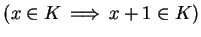 , then
, then
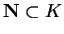 .
.




Next: 3.2 Integers and Rationals.
Up: 3. Induction and Integers
Previous: 3. Induction and Integers
Index
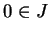 .
.
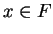 ,
,
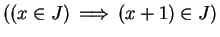 .
.
![]() is an inductive subset of
is an inductive subset of ![]() , then
, then
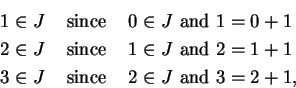
![]() is an inductive subset of
is an inductive subset of
![]() , then
, then
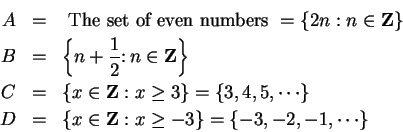
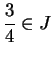 .
.
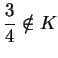 .
.
![]() is in every inductive set,
is in every inductive set,
![]() . Let
. Let ![]() be an inductive
subset of
be an inductive
subset of ![]() . Then for all
. Then for all ![]() ,
,
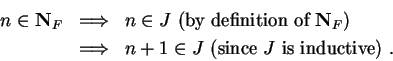
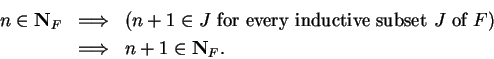
![]() be a proposition form on
be a proposition form on
![]() satisfying (3.11) and
(3.12). Let
satisfying (3.11) and
(3.12). Let
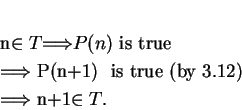
![]() , then
, then ![]() is false, so
is false, so
![]() is true.
is true.
![]() be the proposition form on
be the proposition form on
![]() defined by
defined by
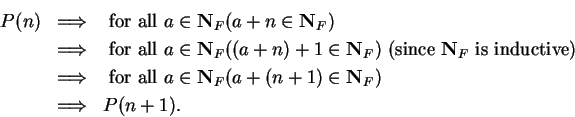
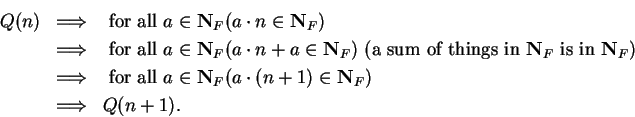
![]() on
on
![]() by
by
![]() on
on
![]() by
by
![]() define a proposition form
define a proposition form ![]() on
on
![]() by
by
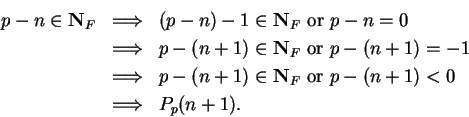
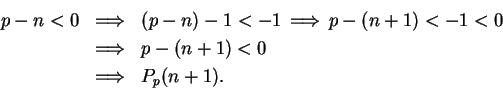
![]() is a subset of
is a subset of
![]() having no least
element, then
having no least
element, then ![]() .
.
![]() be a subset of
be a subset of
![]() having no least element. For each
having no least element. For each
![]() define
a proposition
define
a proposition ![]() by
by
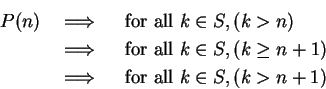
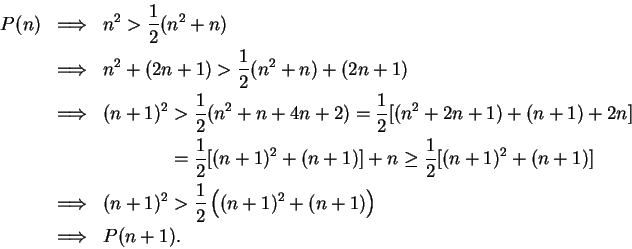
![]() be the proposition form on
be the proposition form on
![]() defined by
defined by
for ``one" signifies a measure of some plurality, and `` a number" signifies a measured plurality or a plurality of measures. Therefore, it is also with good reason that unity is not a number; for neither is a measure measures, but a measure is a principle, and so is unity
. [5, page 237, N, 1, 1088a5]
![]() is called an infinite quantity.
is called an infinite quantity.
![]() (starting with
(starting with ![]() ), one of
which can be paraphrased as: If
), one of
which can be paraphrased as: If ![]() is any set, such that
is any set, such that ![]() and for all
and for all
![]() ,
,
![]() , then
, then
![]() .
.