


Next: 3. Induction and Integers
Up: 2. Fields
Previous: 2.6 Ordered Fields
Index
2.130
Definition (Absolute value.)
Let
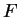
be an ordered field, and let
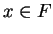
. Then we define
Proof: If 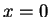 then (2.133) becomes
then (2.133) becomes
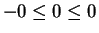 , which is true. If
, which is true. If
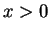 then
then 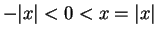 . If
. If 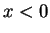 then
then
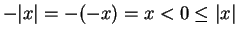 . Hence (2.133) holds in
all cases.
. Hence (2.133) holds in
all cases.
2.134
Exercise.
Let
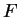
be an ordered field. Prove that
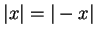
for all
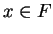
and
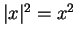
for all
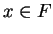
.
2.135
Exercise (Product formula for absolute value.)
A
Prove that for all
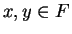
,
Proof: We first show that
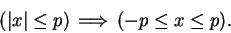 |
(2.139) |
- Case 1.
- If
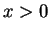 , then
, then
- Case 2.
- If
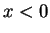 , then
, then
- Case 3.
- If
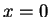 , then
, then
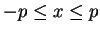 is true, so (2.139) is
true. Hence (2.139) is valid in all cases.
is true, so (2.139) is
true. Hence (2.139) is valid in all cases.
Next we show that
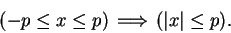 |
(2.140) |
- Case 1.
- If
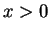 , then
, then
- Case 2.
- If
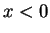 , then
, then
- Case 3.
- If
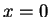 then
then 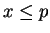 is true, so (2.140) is true. Hence
(2.140) is true in all cases.
is true, so (2.140) is true. Hence
(2.140) is true in all cases.
We have proved (2.137).
Since
 is true if and only if
is true if and only if
 is true,
is true,
i.e.,
This is 2.138.
2.141
Remark.
I leave it to you to check that (
2.137) holds when
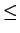
is replaced by
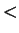
,
and (
2.138) holds when
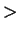
and
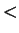
are replaced by
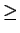
and
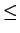
,
respectively.
2.142
Theorem (Triangle inequality.)Let 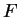 be an ordered field. Then
be an ordered field. Then
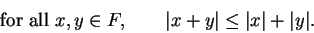 |
(2.143) |
Proof: The obvious way to prove this is by cases. But there are many
cases to consider, e.g. (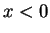 and
and 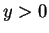 and
and 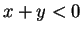 ). I will use an ingenious trick
to avoid the cases. For all
). I will use an ingenious trick
to avoid the cases. For all 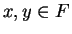 , we have
, we have
and
By adding the inequalities, we get
By theorem 2.136 it follows that
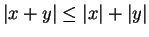 .
.
2.145
Exercise (Quotient formula for absolute value.)
A
Let
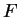
be an ordered field. Let
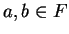
with
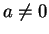
. Show that
- a)
-
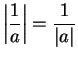 ,
,
- b)
-
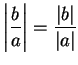 .
.
2.146
Definition (Distance.)
Let
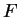
be an ordered field, and let
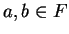
. We define the
distance from
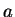 to
to 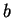
to be
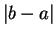
.
2.147
Remark.
If
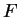
is the ordered field of real or rational numbers,
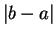
represents the
familiar notion of distance between the points
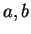
on the real line (or the
rational line).
2.148
Exercise.
Let
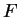
be an ordered field. Let
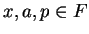
with
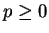
. Show that
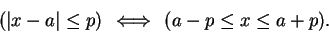 |
(2.149) |
HINT: Use theorem
2.136. Do not reprove theorem
2.136.
2.150
Remark.
We can state the result of exercise
2.148 as follows. Let
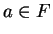
, and let
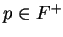
. Then the set of points whose distance from
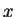
is smaller than
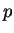
, is
the set of points between
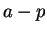
and
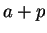
.
2.151
Definition (Intervals and endpoints.)
Let
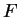
be an ordered field. Let
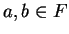
with
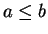
. Then we define
A set that is equal to a set of any of these nine types is called an
interval.
Note that
![$[a,a)=(a,a]=(a,a)=\emptyset$](img707.gif)
and
![$[a,a]=\{a\}$](img708.gif)
, so the empty set is an
interval and so is a set containing just one point. Sets of the first four types
have
endpoints 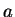
and
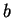
,
except that
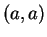
has no endpoints. Sets
of the second four types have just one endpoint, namely
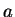
. The interval
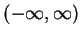
has no endpoints.
2.152
Examples.
Let
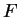
be an ordered field. By exercise
2.148 the set of solutions
to
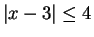
is
I can read this result from the figure by counting 4 units to the left and right of
3. This method is just a way of remembering the result of theorem 2.148.
Now suppose I want to find the solutions in 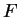 to
to
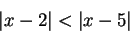 |
(2.153) |
Here, thinking of
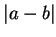
as the distance from
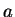
to
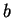
, I want to find all
elements that are nearer to 2 than to 5. From the picture I expect the answer to be
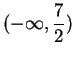
. Although this picture method is totally unjustified by
anything I've done, it is the method I would use to solve the inequality in practice.
If I had to use results we've proved to solve (
2.153), I'd say (since
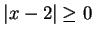
)
which agrees with my answer by picture.
2.154
Exercise.
A
Let
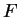
be an ordered field,
let
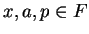
with
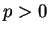
. Show
that
Interpret the result geometrically on a number line.
2.156
Note.
Girolamo Cardano (1501-1576)
, in an attempt
to make sense of the square root of a negative number, proposed an alternate law
of signs in which the product of two numbers is negative if at least one
factor is negative.
He concluded that ``plus divided by plus gives plus'', and ``minus divided by
plus gives minus'', but ``plus divided by minus gives nothing'' (i.e. zero),
since both of the assertions ``plus divided by minus gives plus'' and ``plus
divided by minus gives minus'' are contradictory.[
40, p 25]
I believe that our axioms for an ordered field are due to Artin and Schreier in 1926
[6, page 259].
Systems satisfying various combinations of algebraic and order axioms were considered
by Huntington [28] in 1903.
The notation 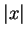 for absolute value was introduced by Weierstrass in
1841[15, vol.2, page 123]. It was first introduced for complex numbers
rather than real numbers.
for absolute value was introduced by Weierstrass in
1841[15, vol.2, page 123]. It was first introduced for complex numbers
rather than real numbers.



Next: 3. Induction and Integers
Up: 2. Fields
Previous: 2.6 Ordered Fields
Index
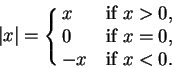
![]() then (2.133) becomes
then (2.133) becomes
![]() , which is true. If
, which is true. If
![]() then
then ![]() . If
. If ![]() then
then
![]() . Hence (2.133) holds in
all cases.
. Hence (2.133) holds in
all cases.
![]()
![]() is true if and only if
is true if and only if
![]() is true,
is true,
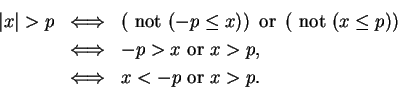
![]() and
and ![]() and
and ![]() ). I will use an ingenious trick
to avoid the cases. For all
). I will use an ingenious trick
to avoid the cases. For all ![]() , we have
, we have
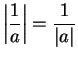 ,
,
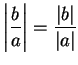 .
.
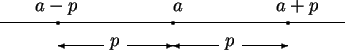
![\begin{eqnarray*}
(a,b) &=& \{x\in F\colon a<x<b\} \\
(a,b{]} &=& \{x\in F\colo...
...\infty) &=& \{x\in F\colon x\geq a\} \\
(-\infty,\infty) &=& F.
\end{eqnarray*}](img706.gif)
![]() to
to
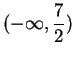 . Although this picture method is totally unjustified by
anything I've done, it is the method I would use to solve the inequality in practice.
If I had to use results we've proved to solve (2.153), I'd say (since
. Although this picture method is totally unjustified by
anything I've done, it is the method I would use to solve the inequality in practice.
If I had to use results we've proved to solve (2.153), I'd say (since
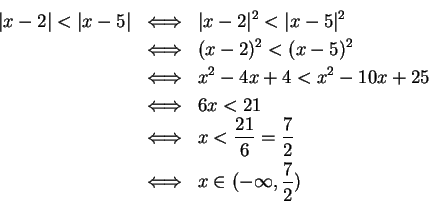
![]() for absolute value was introduced by Weierstrass in
1841[15, vol.2, page 123]. It was first introduced for complex numbers
rather than real numbers.
for absolute value was introduced by Weierstrass in
1841[15, vol.2, page 123]. It was first introduced for complex numbers
rather than real numbers.