Let
![]() be the set of all sets, let
be the set of all sets, let
![]() be the set of all infinite sets,
and let
be the set of all infinite sets,
and let
![]() be the set of all finite sets. Then we have
be the set of all finite sets. Then we have
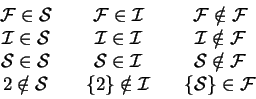
Here
![]() since there are infinitely many finite sets.
since there are infinitely many finite sets.
![]() since
since
![]() contains just one element, which is the set of all sets. Also
contains just one element, which is the set of all sets. Also
![]() since
since ![]() is not a set. Next, let
is not a set. Next, let
| (1.59) |
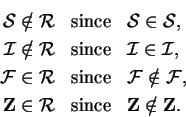
I believe that this paradox has never been satisfactorily explained. A large branch of mathematics (axiomatic set theory) has been developed to get rid of the paradox, but the axiomatic approaches seem to build a fence covered with `` keep out" signs around the paradox rather than explaining it. Observe that the discussion of Russell's paradox does not involve any complicated argument: it lies right on the surface of set theory, and it might cause one to wonder what other paradoxes are lurking in a mathematics based on set theory.
The poet and grammarian Philitas of Cos is even said to have died prematurely from exhaustion, owing to his desperate efforts to solve the paradox.[9, page 493]
Philitas was concerned about a different paradox, but Russell's paradox is probably more deadly.