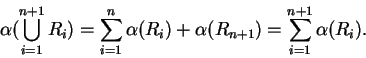Next: C. Prerequisites
Up: Math 111 Calculus I
Previous: A. Hints and Answers
Index
B. Proofs of Some Area Theorems
B.1
Theorem (Addition Theorem.) For any bounded sets  and
and  in
in

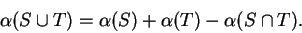 |
(B.2) |
and consequently
Proof: We have
and
Hence by the additivity of area
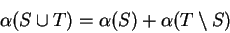 |
(B.3) |
and
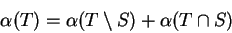 |
(B.4) |
If we solve equation (B.4) for
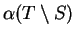 and use this result
in
equation (B.3) we get the desired result.
and use this result
in
equation (B.3) we get the desired result. 
Proof: The proof is by induction. If 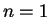 , then (B.6) says
, then (B.6) says
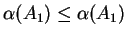 , which is true. Suppose now that
, which is true. Suppose now that 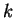 is a generic element of
is a generic element of
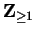 , and that (B.6)
is true when
, and that (B.6)
is true when 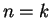 .
Let
.
Let
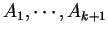 be bounded sets in
be bounded sets in
 . Then
. Then
Hence (B.6) is true when 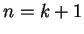 , and by induction
the formula holds for all
, and by induction
the formula holds for all
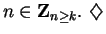
B.7
Theorem (Monotonicity of Area.)
Let 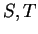 be bounded sets such that
be bounded sets such that 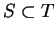 . Then
. Then
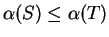 .
.
Proof: If 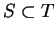 then
then 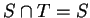 , and in this case
equation (B.4)
becomes
, and in this case
equation (B.4)
becomes
Since
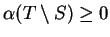 , it follows that
, it follows that
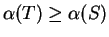 .
. 
Proof: The proof is by induction on  . For
. For 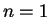 , equation (B.9)
says
that
, equation (B.9)
says
that
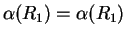 , and this is true. Now suppose
, and this is true. Now suppose
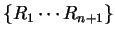 is a family of mutually almost-disjoint sets. Then
is a family of mutually almost-disjoint sets. Then
and this is a finite union of zero-area sets, and hence is a zero-area set.
Hence,
by the addition theorem,
i.e.,
The theorem now follows from the induction principle. 




Next: Prerequisites
Up: Math 111 Calculus I
Previous: A. Hints and Answers
Index
Ray Mayer
2007-09-07
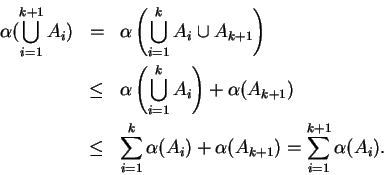
![]() then
then ![]() , and in this case
equation (B.4)
becomes
, and in this case
equation (B.4)
becomes
![]() . For
. For ![]() , equation (B.9)
says
that
, equation (B.9)
says
that
![]() , and this is true. Now suppose
, and this is true. Now suppose
![]() is a family of mutually almost-disjoint sets. Then
is a family of mutually almost-disjoint sets. Then