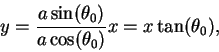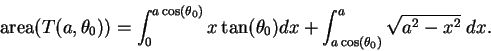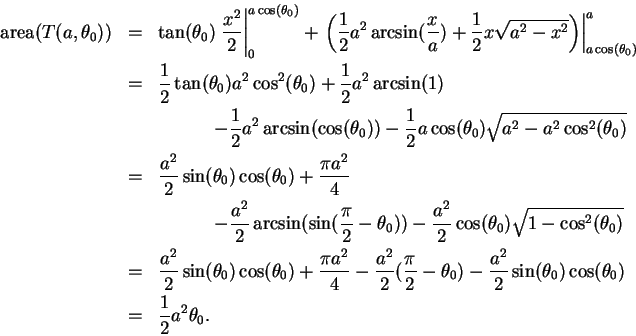Next: 17.6 Substitution in Integrals
Up: 17. Antidifferentiation Techniques
Previous: 17.4 Integration by Substitution
Index
17.5 Trigonometric Substitution
Integrals of the form
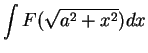 and
and
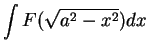 often arise in applications. There is a special trick for dealing with such
integrals. Since
often arise in applications. There is a special trick for dealing with such
integrals. Since
we can write
If we now make the substitution
then we find
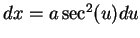 , or
, or
Now
so
(Since
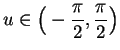 we have
we have 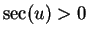 and
the square root is positive.)
Thus
and
the square root is positive.)
Thus
Often this last antiderivative can be found. If
then by the ritual (17.37)
The ritual
to apply when using
this
method for finding
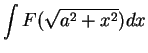 is:
is:
Let 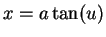 . Then
. Then
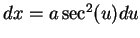 , and
, and
so
There is a similar ritual for
integrals of the form
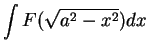 (Here we will
just describe the ritual).
(Here we will
just describe the ritual).
Let 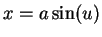 . Then
. Then
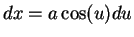 and
and
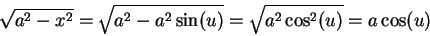 |
(17.43) |
so
Observe that in equation (17.43) we are assuming that
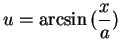 , so
, so
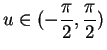 , so
, so
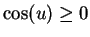 , and the sign of the square root is correct.
, and the sign of the square root is correct.
17.44
Example.
Find
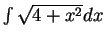
.
Let
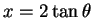 . Then
. Then
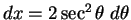 , and
, and
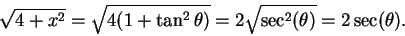 |
(17.45) |
Thus
To find
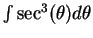
, I will integrate by parts.
Let
Hence,
Hence
i.e.,
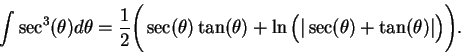 |
(17.46) |
Hence
By (
17.45) we have
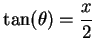
and
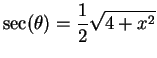
.
Thus
17.47
Example.
In the process of working out the last example
we found
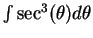
using integration by parts. Here
is a different tricky way of finding the same integral [
32].
17.48
Example.
Find
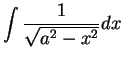
.
Let
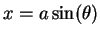 . Then
. Then
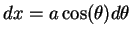 and
and
Thus
17.49
Exercise.
Find the following antiderivatives:
- a)
-
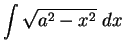
- b)
-
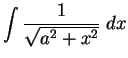
- c)
-
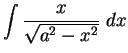
- d)
-
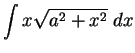 A
A
17.50
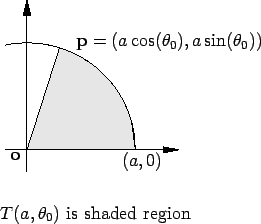
Example (Area of a circular sector)
Let

be a positive number, and let
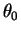
be a number in
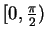
. Let
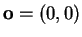
, and let
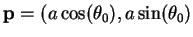
. Let
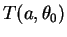
be
the circular sector bounded by the positive

-axis,
the segment
![$[{\bf op]}$](img4276.gif)
, and
the circle
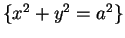
.
The equation for
![$[{\bf op}]$](img4279.gif)
is
and the equation for the upper semicircle is
Hence
where
i.e.
In exercise
17.49A.a you showed that
so
By using symmetry arguments, you can show that this formula actually
holds for
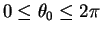
.




Next: 17.6 Substitution in Integrals
Up: 17. Antidifferentiation Techniques
Previous: 17.4 Integration by Substitution
Index
Ray Mayer
2007-09-07
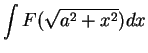 and
and
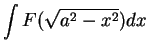 often arise in applications. There is a special trick for dealing with such
integrals. Since
often arise in applications. There is a special trick for dealing with such
integrals. Since
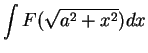 and
and
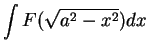 often arise in applications. There is a special trick for dealing with such
integrals. Since
often arise in applications. There is a special trick for dealing with such
integrals. Since
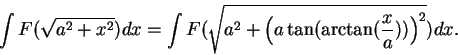
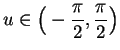 we have
we have 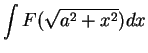 is:
is:
![]() . Then
. Then
![]() , and
, and
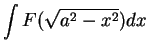 (Here we will
just describe the ritual).
(Here we will
just describe the ritual).
![]() . Then
. Then
![]() and
and
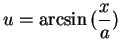 , so
, so
 , so
, so
![]() , and the sign of the square root is correct.
, and the sign of the square root is correct.
![]() . Then
. Then
![]() , and
, and
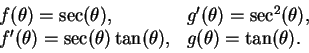
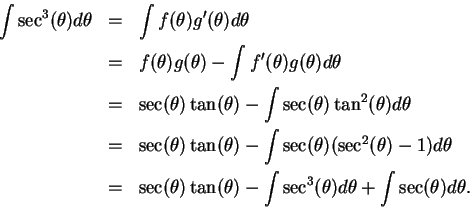
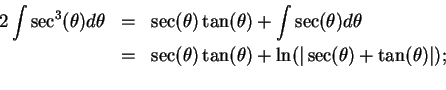
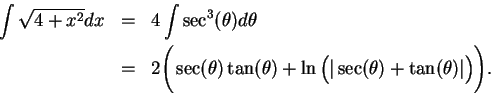
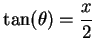 and
and
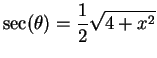 .
Thus
.
Thus
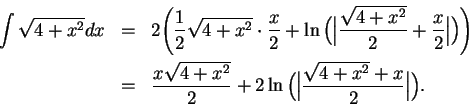
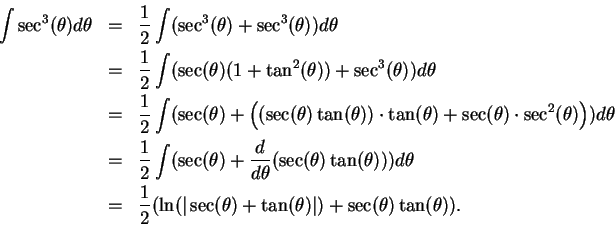
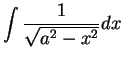 .
.
![]() . Then
. Then
![]() and
and
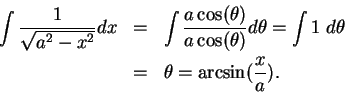
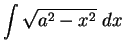
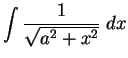
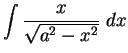
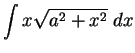 A
A