exists. In this case we denote the limit in (10.19) by
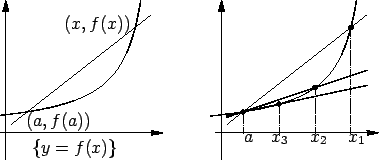
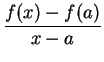 represents the slope of the line
joining the points
represents the slope of the line
joining the points
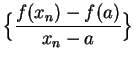 converge to a number
converge to a number
Remark: This definition will need to be generalized later to apply to curves that are not graphs of functions. Also this definition does not allow vertical lines to be tangents, whereas on geometrical grounds, vertical tangents are quite reasonable.
Let ![]() . Then for all
. Then for all
![]() ,
,
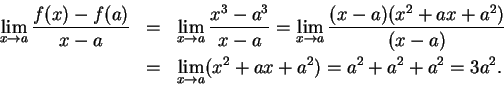
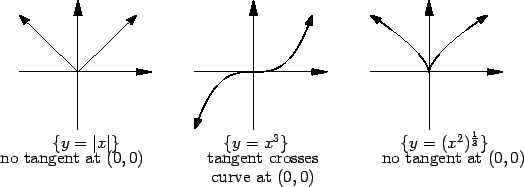
We saw in example 10.10 that
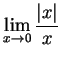 does
not
exist. Hence, the graph of
does
not
exist. Hence, the graph of ![]() at
at ![]() has no tangent.
has no tangent.
If ![]() , then in the previous example we saw that the equation of the
tangent
to graph
, then in the previous example we saw that the equation of the
tangent
to graph![]() at
at ![]() is
is ![]() ; i.e., the
; i.e., the ![]() -axis is tangent to the curve.
Note that in this case the tangent line crosses the curve at the point of
tangency.
-axis is tangent to the curve.
Note that in this case the tangent line crosses the curve at the point of
tangency.
If ![]() then for all
then for all
![]() ,
,
Thus at each point on the curve the tangent line coincides with the curve.
Let
![]() . This is not the same as the function
. This is not the same as the function ![]() since
the domain of
since
the domain of ![]() is
is
![]() while the domain of
while the domain of ![]() is
is
![]() . (For
all
. (For
all
![]() we have
we have
![]() where
where ![]() .)
.)
I want to investigate
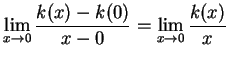 . From the picture, I expect this graph to have an infinite
slope at
. From the picture, I expect this graph to have an infinite
slope at ![]() , which means according to our definition that there is no
tangent
line at
, which means according to our definition that there is no
tangent
line at ![]() . Let
. Let
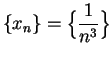 . Then
. Then
![]() , but
, but
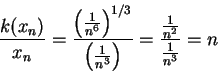
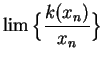 does not exist and hence
does not exist and hence
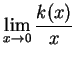 does not exist.
does not exist.
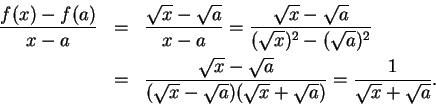
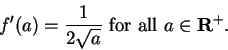
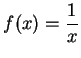 . Sketch the graph of
. Sketch the graph of
Calculate ![]() for arbitrary
for arbitrary
![]() . Does your answer agree with
your
prediction?
. Does your answer agree with
your
prediction?
On what intervals do you expect ![]() to be positive? On what intervals do
you
expect
to be positive? On what intervals do
you
expect ![]() to be negative? Calculate
to be negative? Calculate ![]() .
.
On the basis of symmetry, what do you expect to be the values of ![]() ,
,
![]() and
and ![]() ? For what
? For what ![]() do you expect
do you expect ![]() to be zero? On
the
basis of your guesses and your calculated value of
to be zero? On
the
basis of your guesses and your calculated value of ![]() , draw a graph of
, draw a graph of
![]() ,
where
,
where ![]() is the function that assigns
is the function that assigns ![]() to a generic number
to a generic number ![]() in
in
![]() . On the basis of your graph, guess a formula for
. On the basis of your graph, guess a formula for ![]() .
.
(Optional) Prove that your guess is correct. (Some trigonometric identities will be needed.)
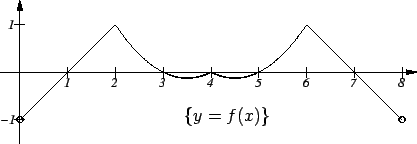
For what ![]() in
in ![]() does
does ![]() exist? Sketch the graphs
of
exist? Sketch the graphs
of ![]() and
and ![]() on the same set of axes.
on the same set of axes.
The following definition which involves time and motion and particles is not a part of our official development and will not be used for proving any theorems.
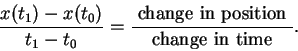
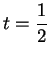 ,
and
then back to
,
and
then back to
The instantaneous velocity
of
![]() at a time
at a time ![]() is defined to be
is defined to be
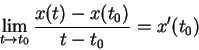
In applications we will usually express velocity in units like
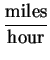 . We will wait until we have developed some
techniques for differentiation before we do any velocity problems.
. We will wait until we have developed some
techniques for differentiation before we do any velocity problems.
The definition of velocity just given would have made no sense to Euclid or Aristotle. The Greek theory of proportion does not allow one to divide a length by a time, and Aristotle would no more divide a length by a time than he would add them. Question: Why is it that today in physics you are allowed to divide a length by a time, but you are not allowed to add a length to a time?
In Newton's calculus, the notion of instantaneous velocity or fluxion was taken as an undefined, intuitively understood concept, and the fluxions were calculated using methods similar to that used in the section 10.1.
The first ``rigorous'' definitions of limit of a function were given around 1820 by Bernard Bolzano (1781-1848) and Augustin Cauchy (1789-1857)[23, chapter 1]. The definition of limit of a function in terms of limits of sequences was given by Eduard Heine in 1872.