Proof: Let ![]() be any interval in
be any interval in
![]() . Then
. Then ![]() is piecewise
monotonic on
is piecewise
monotonic on ![]() and hence is integrable. Let
and hence is integrable. Let
![]() be
the regular partition of
be
the regular partition of ![]() into
into ![]() equal subintervals, and let
equal subintervals, and let
Let
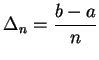 so that
so that
![]() and
and
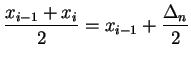 for
for ![]() . Then
. Then
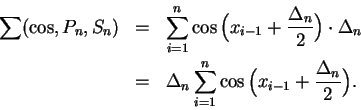
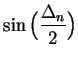 and use
the identity
and use
the identity
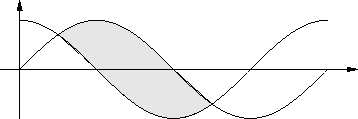
![\begin{eqnarray*}
\sin\Big({{\Delta_n}\over 2}\Big)\sum(\cos,P_n,S_n) &=&
\Delta...
...-\sin(x_0)]\\
&=& {{\Delta_n}\over 2}\Big(\sin(b)-\sin(a)\Big).
\end{eqnarray*}](img2518.gif)
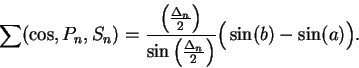
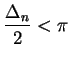 , and
then
, and
then
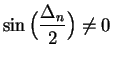 , so we haven't divided
by
, so we haven't divided
by
 is the same as in that proof.
is the same as in that proof.
Proof: We will prove the first formula. The proof of the second is similar.
If ![]() then the conclusion follows from theorem 9.43.
then the conclusion follows from theorem 9.43.
If ![]() then
then
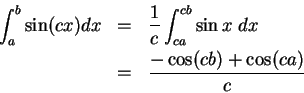
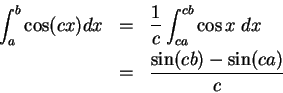
Statement A:
If a polygon be inscribed in a segment of a circleso that all its sides excluding the base are equal and their number even, as
,
being the middle point of segment, and if the lines
,
,
parallel to the base
and joining pairs of angular points be drawn, then
whereWe will now show that this result can be reformulated in modern notation as follows.is the middle point of
and
is the diameter through
.[2, page 29]
Statement B:
Let ![]() be a number in
be a number in ![]() , and let
, and let ![]() be a positive integer.
Then there exists a partitition-sample sequence
be a positive integer.
Then there exists a partitition-sample sequence
![]() for
for ![]() ,
such that
,
such that
In exercise (9.56) you are asked to show that
(9.52) implies that
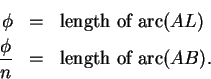
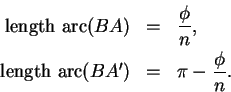
Prove statement A above. Note that (see the figure
below statement A)