



Next: 3.3 Functions
Up: 3. Propositions and Functions
Previous: 3.1 Propositions
Index
The most common way of describing sets is by means of proposition forms.
3.24
Notation (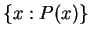 )
)
Let

be a proposition form over a set

, and let
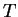
be a subset of

.
Then
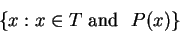 |
(3.25) |
is defined to be the set of all elements

in
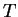
such that
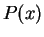
is true.
The set described in (
3.25) is also written
In cases where the meaning of ``
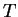
'' is clear from the context, we may
abbreviate (
3.25) by
3.26
Examples.
is the set of all even integers, and
If  and
and 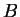 are sets, then
are sets, then
We will use the following notation throughout these notes.
3.30
Notation (
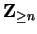 ,
,
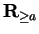 )
)
If

is an
integer we define
Thus
Similarly, if

is a real number, we define
3.31
Definition (Ordered pair.)
If
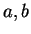
are objects, then the
ordered pair 
is a
new object obtained by combining
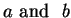
. Two ordered
pairs
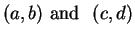
are equal if and only if
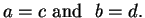
Similarly we may consider
ordered triples. Two ordered triples
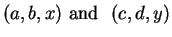
are equal if and only if
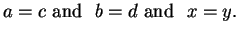
We use the same notation

to represent an open interval in
and
an ordered pair in

. The context should always make it clear
which meaning is intended.
3.32
Definition (Cartesian product)
If
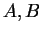
are sets then the
Cartesian product of  and
and 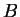
is defined to be the set of all ordered pairs
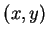
such that
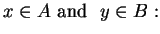
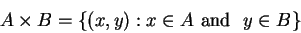 |
(3.33) |
3.34
Examples.
Let
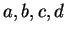
be real numbers with
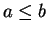
and
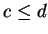
.
Then
and
Thus in general
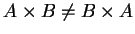
.
The set 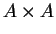 is denoted by
is denoted by 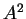 . You are familiar with one
Cartesian product. The euclidean plane
. You are familiar with one
Cartesian product. The euclidean plane
 is the Cartesian
product of R with itself.
is the Cartesian
product of R with itself.
3.35
Exercise.
Let
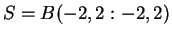
and let
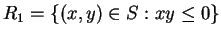
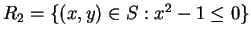
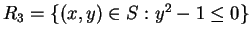
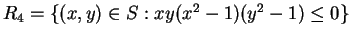
Sketch the sets
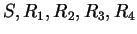 . For
. For 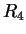 you should include an
explanation of how you arrived at your answer. For the other sets
no explanation is required.
you should include an
explanation of how you arrived at your answer. For the other sets
no explanation is required.
3.36
Exercise.
Do there exist sets
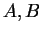
such that
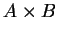
has
exactly five elements?




Next: 3.3 Functions
Up: 3. Propositions and Functions
Previous: 3.1 Propositions
Index
Ray Mayer
2007-09-07
![]() and
and ![]() are sets, then
are sets, then
![]() is denoted by
is denoted by ![]() . You are familiar with one
Cartesian product. The euclidean plane
. You are familiar with one
Cartesian product. The euclidean plane
![]() is the Cartesian
product of R with itself.
is the Cartesian
product of R with itself.
![]()
![]()
![]()
![]()
![]() . For
. For ![]() you should include an
explanation of how you arrived at your answer. For the other sets
no explanation is required.
you should include an
explanation of how you arrived at your answer. For the other sets
no explanation is required.