

Next: Area formulas
Up: C. Prerequisites
Previous: Order Laws
Names for Rational Numbers:
Every rational number 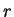 can be written as a quotient of integers:
can be written as a quotient of integers:
and without loss of generality we may take 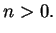 In general, a rational number has many different
names, e.g.
In general, a rational number has many different
names, e.g.
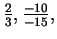 and
and 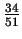 are
different names for the same rational number. If I say
``let
are
different names for the same rational number. If I say
``let
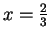 '', I mean let
'', I mean let 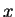 denote the rational number
which has ``
denote the rational number
which has ``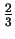 '' as one of its names. You should think of
each rational number as a specific point on the line of real numbers.
Let
'' as one of its names. You should think of
each rational number as a specific point on the line of real numbers.
Let 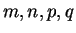 be integers with
be integers with
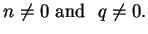 Then
Then
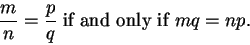 |
(C.80) |
If 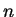 and
and 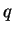 are positive, then
are positive, then
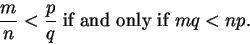 |
(C.81) |
Equations C.80 and C.81 hold for arbitrary
real numbers 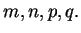 It will be assumed that if you are given
two rational numbers, you can decide whether or not the first is less
that the second. You also know that the sum, difference, and product
of two integers is an integer, and the additive inverse of an integer
is an integer.
It will be assumed that if you are given
two rational numbers, you can decide whether or not the first is less
that the second. You also know that the sum, difference, and product
of two integers is an integer, and the additive inverse of an integer
is an integer.
Absolute value: If 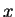 is a real number, then the absolute
value of
is a real number, then the absolute
value of 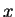 , denoted by
, denoted by 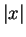 , is defined by
, is defined by
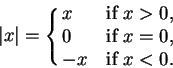 |
(C.82) |
For all real numbers 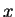 and all positive numbers
and all positive numbers 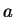 we have
we have
For all real numbers 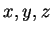 with
with 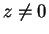 ,
,
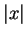 |
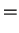 |
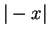 |
(C.85) |
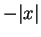 |
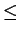 |
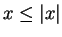 |
(C.86) |
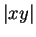 |
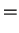 |
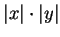 |
(C.87) |
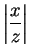 |
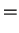 |
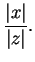 |
(C.88) |
Powers: If 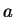 is a real number, and
is a real number, and 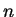 is a non-negative
integer, then
the power
is a non-negative
integer, then
the power 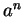 is defined by the rules
is defined by the rules
If 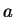 is a non-zero number and
is a non-zero number and 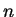 is a negative integer, then
is a negative integer, then 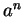 is defined by
is defined by
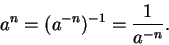 |
(C.91) |
If 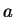 is a non-negative number and
is a non-negative number and 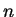 is a positive integer,
then
is a positive integer,
then
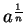 is defined by
is defined by
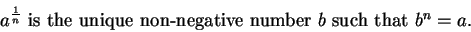 |
(C.92) |
If 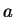 is a non-negative number and
is a non-negative number and 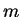 is an arbitrary integer and
is an arbitrary integer and
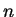 is a positive integer, then
is a positive integer, then 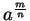 is defined by
is defined by
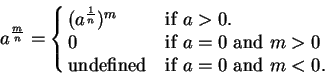 |
(C.93) |
If 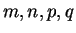 are integers such that
are integers such that 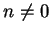 and
and 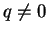 and
and
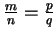 , then
, then
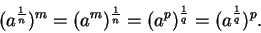 |
(C.94) |
Monotonicity of Powers: If 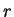 is a positive rational
number, and
is a positive rational
number, and 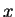 and
and 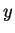 are non-negative real numbers, then
are non-negative real numbers, then
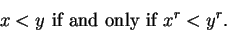 |
(C.95) |
If 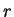 is a negative rational number, and
is a negative rational number, and 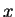 and
and 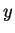 are positive
real numbers, then
are positive
real numbers, then
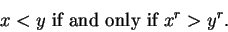 |
(C.96) |
If 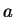 is a positive real number greater than 1, and
is a positive real number greater than 1, and 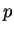 and
and 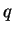 are
rational numbers,
then
are
rational numbers,
then
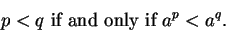 |
(C.97) |
If 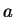 is a positive real number less than 1, and
is a positive real number less than 1, and 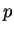 and
and 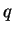 are
rational numbers, then
are
rational numbers, then
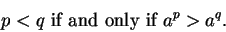 |
(C.98) |
Laws of exponents: Let 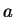 and
and 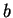 be real numbers, and let
be real numbers, and let 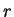 and
and 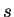 be rational numbers. Then the following relations hold whenever
all of the powers involved are defined:
be rational numbers. Then the following relations hold whenever
all of the powers involved are defined:
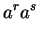 |
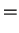 |
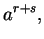 |
(C.99) |
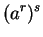 |
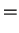 |
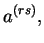 |
(C.100) |
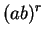 |
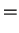 |
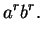 |
(C.101) |
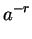 |
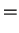 |
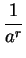 |
(C.102) |
Remarks on equality: If
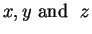 are
names for mathematical objects,
then we write
are
names for mathematical objects,
then we write 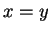 to mean that
to mean that 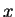 and
and 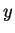 are different names for the
same object. Thus
are different names for the
same object. Thus
 |
(C.103) |
and it is always the case that
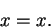 |
(C.104) |
It also follows that
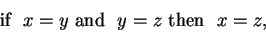 |
(C.105) |
and more generally,
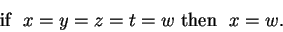 |
(C.106) |
If 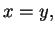 then the name
then the name 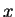 can be substituted for the name
can be substituted for the name 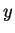 in
any statement containing the name
in
any statement containing the name 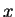 . For example, if
. For example, if 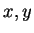 are numbers
and we know that
are numbers
and we know that
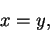 |
(C.107) |
then we can conclude that
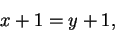 |
(C.108) |
and that
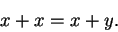 |
(C.109) |
When giving a proof, one ordinarily goes from an equation such as C.107
to equations such as C.108 or C.109 without
mentioning the reason, and the properties C.103-C.106
are usually used without mentioning them explicitly.


Next: Area formulas
Up: C. Prerequisites
Previous: Order Laws
Ray Mayer
2007-08-31
![]() can be written as a quotient of integers:
can be written as a quotient of integers:
![]() It will be assumed that if you are given
two rational numbers, you can decide whether or not the first is less
that the second. You also know that the sum, difference, and product
of two integers is an integer, and the additive inverse of an integer
is an integer.
It will be assumed that if you are given
two rational numbers, you can decide whether or not the first is less
that the second. You also know that the sum, difference, and product
of two integers is an integer, and the additive inverse of an integer
is an integer.
![]() is a real number, then the absolute
value of
is a real number, then the absolute
value of ![]() , denoted by
, denoted by ![]() , is defined by
, is defined by
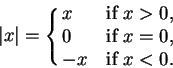
![]() and all positive numbers
and all positive numbers ![]() we have
we have
![]() is a non-zero number and
is a non-zero number and ![]() is a negative integer, then
is a negative integer, then ![]() is defined by
is defined by
![]() is a non-negative number and
is a non-negative number and ![]() is a positive integer,
then
is a positive integer,
then
![]() is defined by
is defined by
![]() is a non-negative number and
is a non-negative number and ![]() is an arbitrary integer and
is an arbitrary integer and
![]() is a positive integer, then
is a positive integer, then ![]() is defined by
is defined by
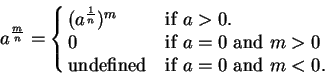
![]() are integers such that
are integers such that ![]() and
and ![]() and
and
![]() , then
, then
![]() is a positive rational
number, and
is a positive rational
number, and ![]() and
and ![]() are non-negative real numbers, then
are non-negative real numbers, then
![]() and
and ![]() be real numbers, and let
be real numbers, and let ![]() and
and ![]() be rational numbers. Then the following relations hold whenever
all of the powers involved are defined:
be rational numbers. Then the following relations hold whenever
all of the powers involved are defined:
![]() are
names for mathematical objects,
then we write
are
names for mathematical objects,
then we write ![]() to mean that
to mean that ![]() and
and ![]() are different names for the
same object. Thus
are different names for the
same object. Thus