Here are my
- slides [Warning: 9.6MB PDF]
Most of the content is drawn from Christophe Cazanave's very readable paper Algebraic homotopy classes of rational functions.
Below, you'll find several animations that illustrate what an algebraic deformation (more properly, naive A1-homotopy) is and is not. See pages 14 and 15 of the slides for formulas.
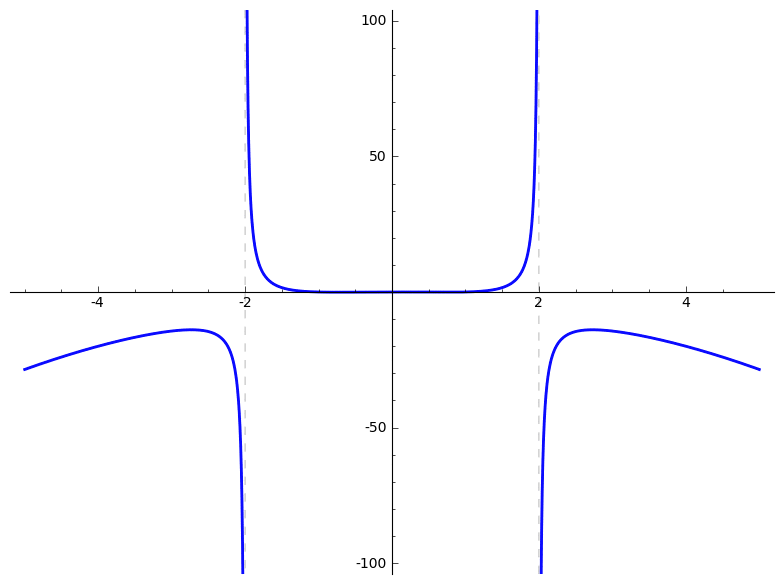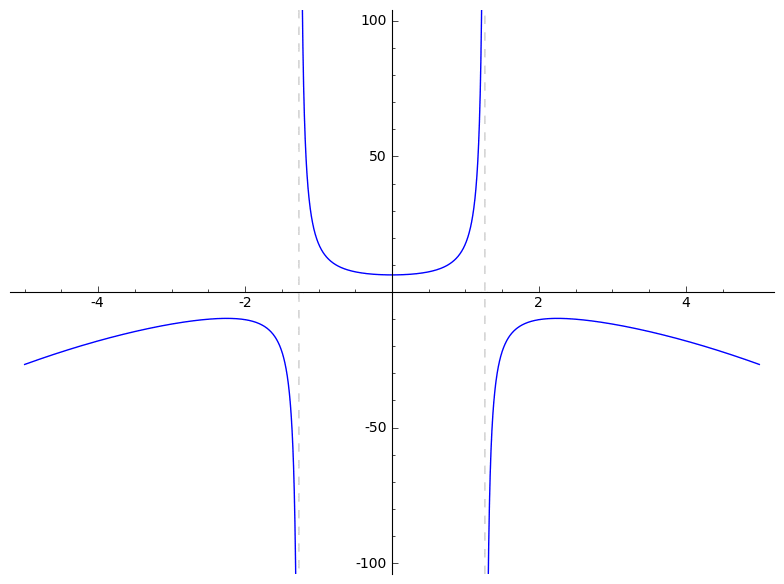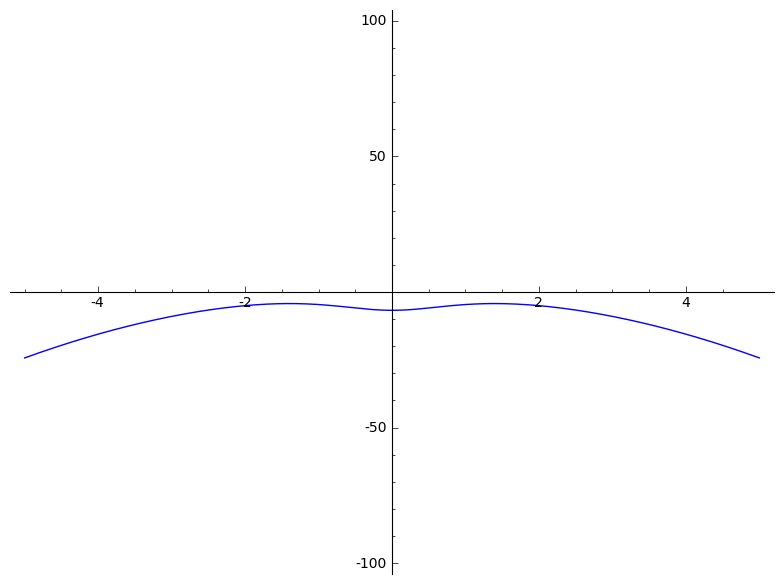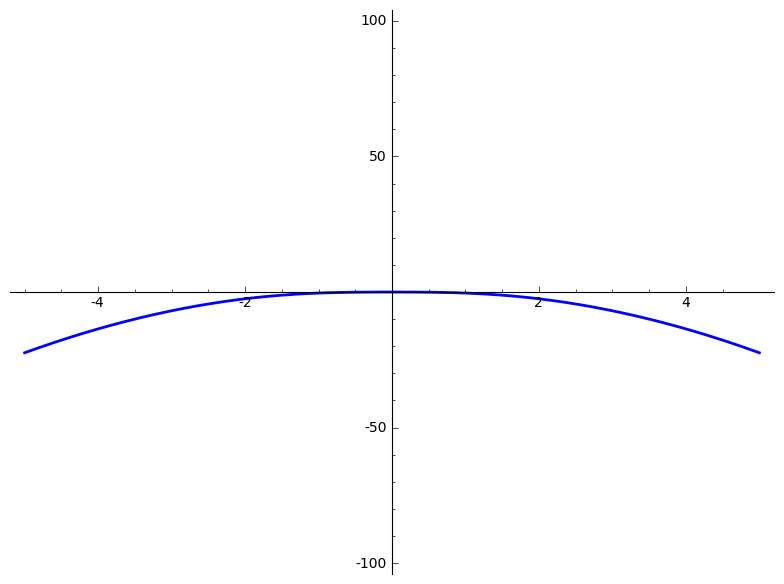
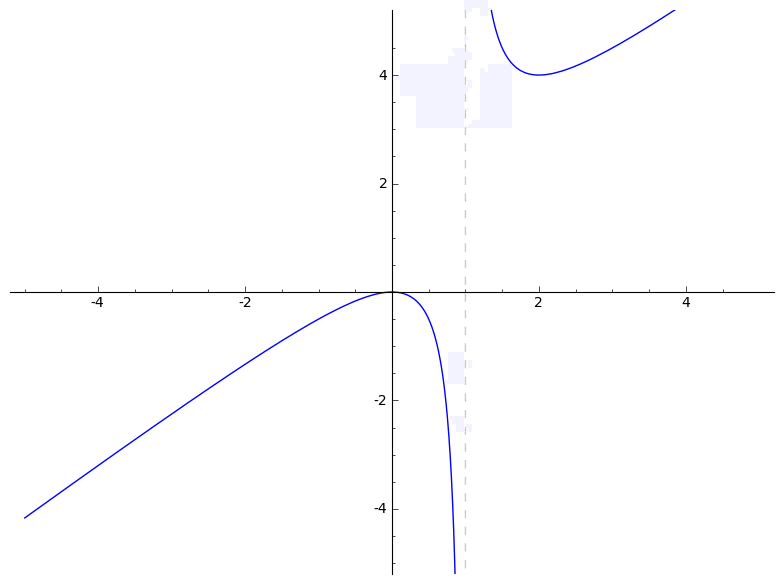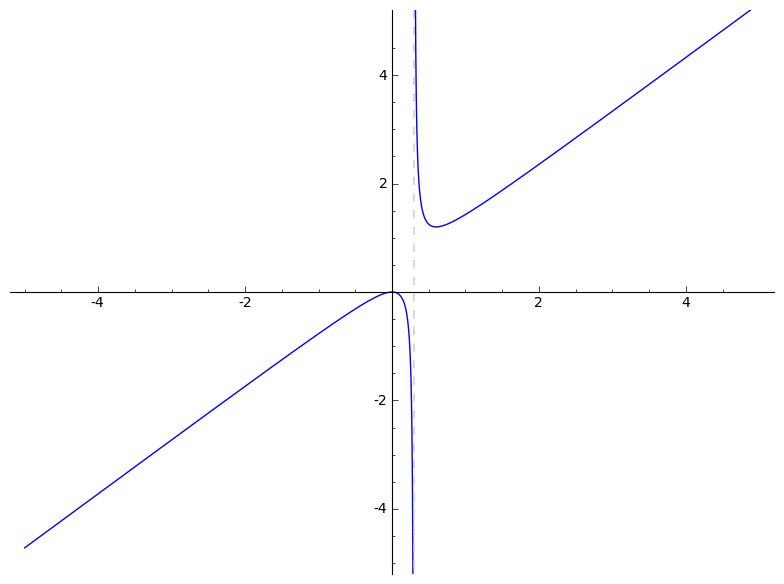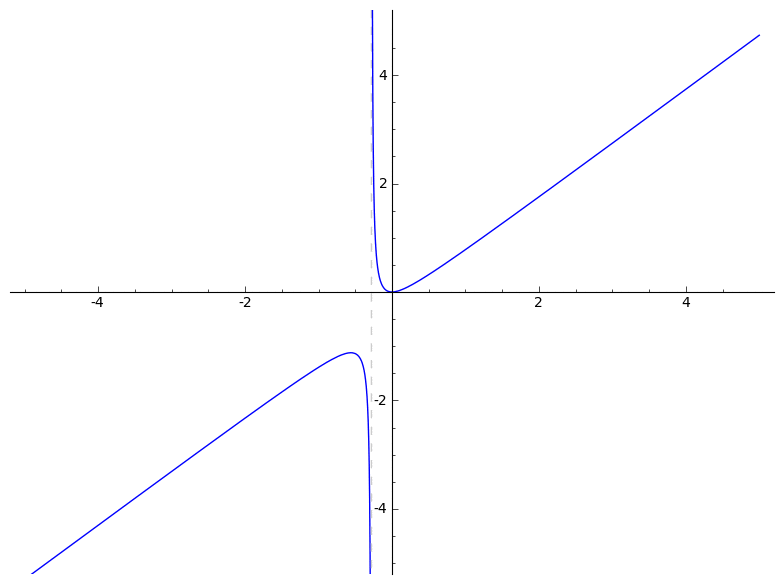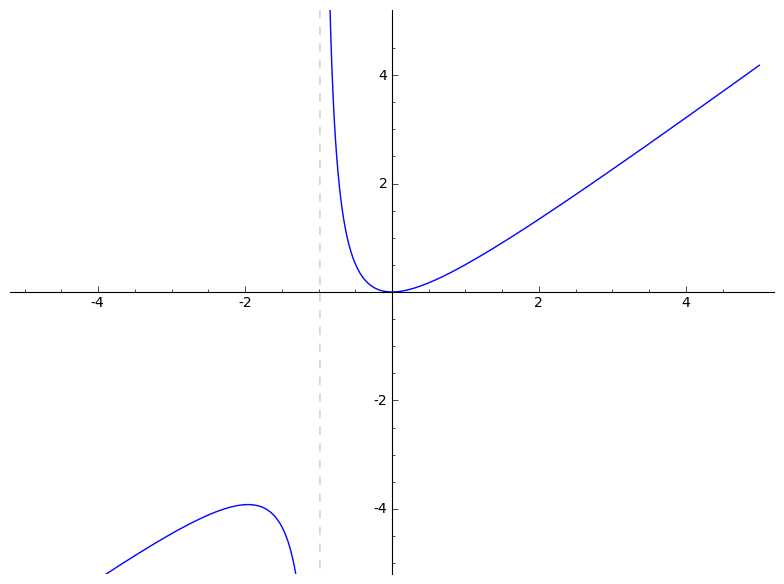
To construct examples of homotopies, you can apply Cazanave's monoid law to some very boring homotopies. Cf. Section 3 of Algebraic homotopy classes of rational functions for information on the monoid law. I wrote the following very basic Magma code to implement the monoid law:
The animations themselves were then produced in sage.
Additionally, the function "TCtFrac(P,Q)" can be used to compute Cazanave's twisted continued fraction representation of a pointed rational function P/Q (cf. Example 3.3 of his paper).
Motivic homotopy theory poses and answers a lot of questions about quadratic forms. If you're interested in learning more about quadratic forms, I highly recommend
- T.Y. Lam, Introduction to quadratic forms over fields.
If you're interested in learning more about motivic homotopy theory, I should warn you that the literature is formiddable and dense, and certainly not written with the intention of being digestible by those lacking ironclad stomachs fortified by routine trips to the all-you can eat algebraic topology/geometry/K-theory buffet. One possible place to begin is
- Marc Levine, Motivic homotopy theory.
Go back home.