Next: 11.2 Convergence Tests
Up: 11. Infinite Series
Previous: 11. Infinite Series
Index
11.1
Definition (Series operator.)
If

is a complex sequence, we define a new sequence
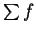
by
or
We use variations, such as
is actually a function that maps complex sequences to complex sequences. We
call
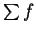
the
series corresponding to

.
11.2
Remark.
If

are complex sequences and
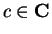
, then
and
since for all

,
and
11.3
Examples.
If
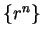
is a geometric sequence,
then
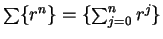
is a
sequence we have been calling a geometric series.
If
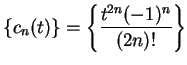
, then
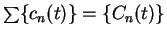
is the sequence for
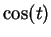
that we
studied in the last chapter.
11.4
Definition (Summable sequence.)
A complex sequence
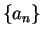
is
summable
if and only if the series
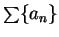
is convergent. If
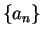
is summable, we denote
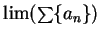
by
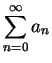
. We call
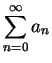
the
sum of
the series
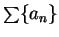
.
11.5
Example.
If
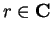
and
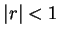
, then
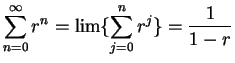
.
11.6
Example (Harmonic series.)
The series
is called the
harmonic series,
and is denoted by
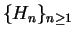
. Thus
We will show that
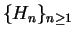
diverges; i.e., the sequence
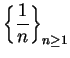
is not summable. For all
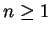
, we have
From the relation
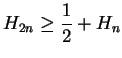
, we have
and (by induction),
Hence,
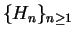
is not bounded, and thus
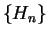
diverges; i.e.,
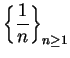
is not summable.
Proof: The proof is left to you.
11.8
Exercise.
Let

be summable sequences. Show that
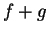
is summable and that
11.9
Example.
The product of two summable sequences is not necessarily summable. If
then
This is a null sequence, so

is summable and
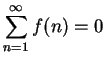
.
However,
so
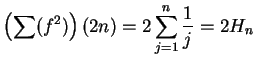
. Thus
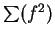
is
unbounded and hence
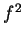
is not summable.
11.10
Theorem.
Every summable sequence is a null sequence. [The converse is not true. The harmonic
series provides a counterexample.]
Proof: Let  be a summable sequence. Then
be a summable sequence. Then
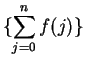 converges to
a limit
converges to
a limit 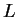 , and by the translation theorem
, and by the translation theorem
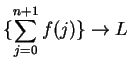 also.
Hence
also.
Hence
i.e.,
and it follows that  is a null sequence.
is a null sequence.





Next: 11.2 Convergence Tests
Up: 11. Infinite Series
Previous: 11. Infinite Series
Index
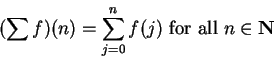
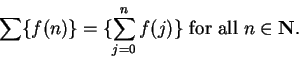
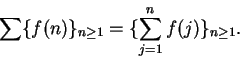
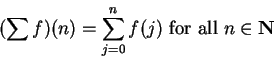
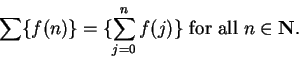
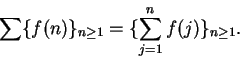
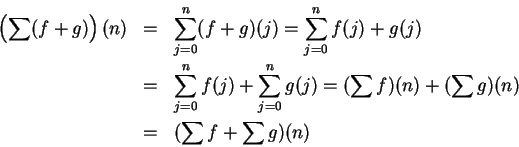
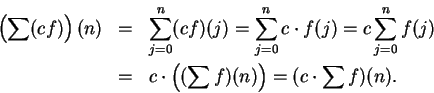
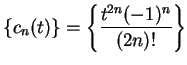 , then
, then
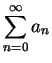 . We call
. We call
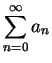 the sum of
the series
the sum of
the series 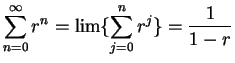 .
.
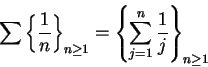
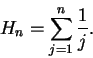
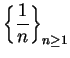 is not summable. For all
is not summable. For all 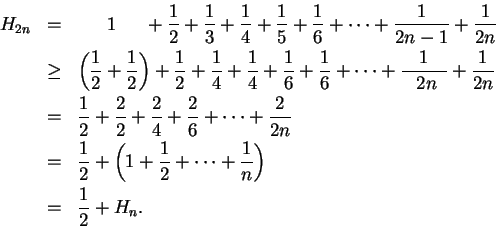
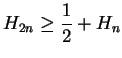 , we have
, we have
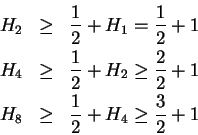
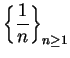 is not summable.
is not summable.
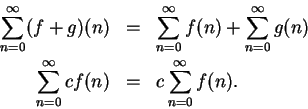
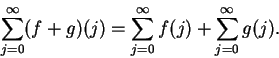
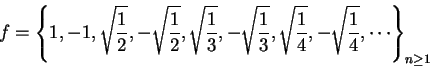
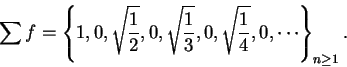
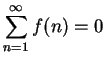 .
However,
.
However,
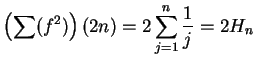 . Thus
. Thus ![]() be a summable sequence. Then
be a summable sequence. Then
 converges to
a limit
converges to
a limit ![]() , and by the translation theorem
, and by the translation theorem
 also.
Hence
also.
Hence