Sandpile Projects Ideas
Acyclic orientations
The paper G-parking functions, acyclic orientations and spanning trees gives a bijection between maximal G-parking functions and acyclic orientations of a graph. A maximal G-parking function is the same as a maximal superstable configuration or a minimal recurrent configuration or a minimal alive configuration.
- Give an exposition of the main result of this paper in terms most closely related to our class.
- Does their idea extend to all recurrents?
- Can the result be modified to account for the minimal recurrents of a directed graph?
Identity Element
Experimentally, one sees that the identity configuration for a rectangular grid graph has a large rectangle inside it, however no one has been able to prove this. Here are some computer experiments that would be interesting.
- How does this result depend on the precise border of the rectangle? What if the border were approximately a rectangle? Would the rectangle inside the identity element disappear?
- Does the result hold in three dimensions (and higher)?
Embedded components
Let 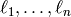 be the columns of the reduced Laplacian matrix for a
sandpile graph
be the columns of the reduced Laplacian matrix for a
sandpile graph 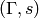 . Define the ideal
. Define the ideal 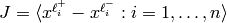 . From the theory of lattice
ideals, we know that the affine toppling ideal,
. From the theory of lattice
ideals, we know that the affine toppling ideal, 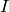 , for
, for 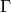 is the
saturation of
is the
saturation of 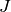 by
by 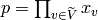 . We also know that
. We also know that
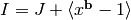 for any burning configuration
for any burning configuration 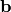 (we
will fix the minimal burning configuration).
(we
will fix the minimal burning configuration).
- Characterize the minimal
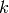 such that
such that 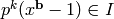 .
. - Let
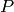 be the embedded component of the primary decomposition of
be the embedded component of the primary decomposition of 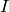 , and let
, and let 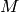 be the ideal generated by the indeterminates. Characterize the minimal
be the ideal generated by the indeterminates. Characterize the minimal 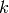 for which
for which 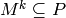 . (One could ask the same question in the homogeneous case, in which one starts with binomial generators corresponding to the columns of the full Laplacian.
. (One could ask the same question in the homogeneous case, in which one starts with binomial generators corresponding to the columns of the full Laplacian.
The Bombay Trick
Consider the sandpile model on a grid. Dhar discovered a way method—called the Bombay trick—by which to count the proportion of recurrent elements that have no sand at a given vertex. The method is described in Height correlations in the Abelian sandpile model and in section 3.7 of Mathematical aspects of the abelian sandpile model. Here is related paper (see page 5).
- Give an exposition of this result.
- Try applying the trick to a different class of graphs.
Riemann-Roch
Investigate how the Riemann-Roch theorem for graphs breaks down for directed graphs. This project would be an expansion of problem 2 from HW 7.
Lattice points in polytopes
To find the complete linear system of a divisor 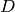 , one must solve a system of
linear inequalities over the integers:
, one must solve a system of
linear inequalities over the integers: 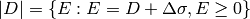 . Geometrically, we are translating the Laplacian lattice by
. Geometrically, we are translating the Laplacian lattice by 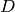 , then intersecting with the positive orthant. The elements of the linear system are then just the lattice points inside of a simplex (I think). One could also consider the collection of scripts
, then intersecting with the positive orthant. The elements of the linear system are then just the lattice points inside of a simplex (I think). One could also consider the collection of scripts 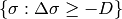 and consider this set of lattice points.
and consider this set of lattice points.
- Compute some examples. Draw some pictures for low-dimensional examples.
- What does Riemann-Roch say in this context?
- What do the formulas for counting lattice points in polytopes say?