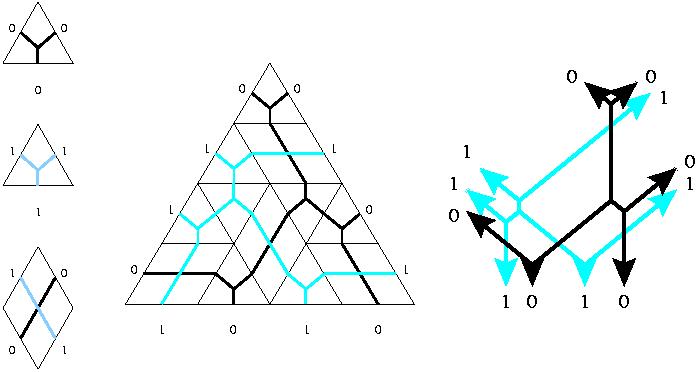
Given the three kinds of puzzle pieces pictured below,
define a puzzle to be a decomposition of a triangle into puzzle pieces
(such that the edges match up, like in a jigsaw puzzle). Call a puzzle
``rigid'' if there is no other puzzle with the same outer boundary.
A lot can be proven about puzzles (we'll do (1) and (2) in the talk):
1. The number of 0s on one side equals the number of 0s on each of
the other two sides - see if you can prove this one before the talk!
2. The lines in the puzzle pieces can all be simultaneously straightened
(as in the right-hand picture below) if and only if the puzzle is rigid
3. There is an easy 1:1 correspondence between rigid puzzles and
inequalities on the eigenvalues of the sum of two Hermitian matrices,
given only the eigenvalues of each one individually
4. The statement ``Given four generic lines in space, there are exactly
two others that touch all four,'' and others like it,
can be turned into puzzle-counting statements.
|

