Welcome to Sage Sandpiles’s documentation!¶
Introduction¶
Sage Sandpiles is a package for calculations involving Dhar’s abelian sandpile model (ASM) using the open-source mathematics software, Sage. A brief introduction to the ASM follows. For a more thorough introduction, the paper Chip-Firing and Rotor-Routing on Directed Graphs [H], by Holroyd et al. is recommended.
To describe the ASM, let 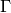 be a directed multigraph with a global sink.
By multigraph, we mean that each edge of
be a directed multigraph with a global sink.
By multigraph, we mean that each edge of 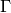 is assigned a nonnegative integer weight, and by global sink, we mean a vertex
is assigned a nonnegative integer weight, and by global sink, we mean a vertex  of out-degree
of out-degree 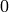 such that every vertex of
such that every vertex of  has a directed path into
has a directed path into  . We denote the vertices of
. We denote the vertices of 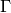 by
by 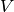 and the nonsink vertices by
and the nonsink vertices by 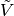 .
.
Configurations and divisors¶
A configuration on 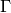 is an element of
is an element of 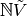 , i.e., the assignment of a nonnegative integer to each nonsink vertex. We think of each integer as a number of grains of sand being placed at the corresponding vertex. A divisor on
, i.e., the assignment of a nonnegative integer to each nonsink vertex. We think of each integer as a number of grains of sand being placed at the corresponding vertex. A divisor on 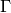 is an element of
is an element of 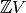 , i.e., an element in the free abelian group on all of the vertices. In the context of divisors, it is sometimes useful to think of assigning dollars to each vertex, with negative integers signifying a debt.
, i.e., an element in the free abelian group on all of the vertices. In the context of divisors, it is sometimes useful to think of assigning dollars to each vertex, with negative integers signifying a debt.
Stabilization¶
A configuration  is stable at a vertex
is stable at a vertex 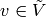 if
if
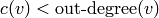 , and
, and  itself is stable if it is stable at each
nonsink vertex. If
itself is stable if it is stable at each
nonsink vertex. If  is unstable at
is unstable at  , the vertex
, the vertex  can be fired
(toppled) by removing
can be fired
(toppled) by removing 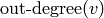 grains of sand from
grains of sand from  and
adding grains of sand to the neighbors of sand, determined by the weights of
the edges leaving
and
adding grains of sand to the neighbors of sand, determined by the weights of
the edges leaving  .
.
Example. Consider the graph:
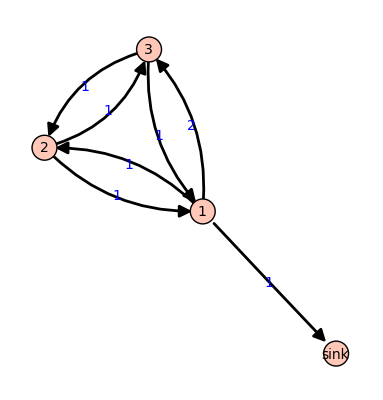
All edges have weight 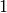 except for the edge from vertex 1 to vertex 3,
which have weight
except for the edge from vertex 1 to vertex 3,
which have weight 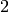 . If we let
. If we let 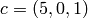 with the indicated number of
grains of sand on vertices 1, 2, and 3, respectively, then only vertex 1,
whose out-degree is 4, is unstable. Firing vertex 1 gives a new
configuration
with the indicated number of
grains of sand on vertices 1, 2, and 3, respectively, then only vertex 1,
whose out-degree is 4, is unstable. Firing vertex 1 gives a new
configuration 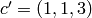 . Here,
. Here, 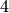 grains have left vertex 1. One of
these has gone to the sink vertex (and forgotten), one has gone to vertex 1,
and two have gone to vertex 2, since the edge from 1 to 2 has weight 2.
Vertex 3 in the new configuration is now unstable. The Sage code for this
example looks like this:
grains have left vertex 1. One of
these has gone to the sink vertex (and forgotten), one has gone to vertex 1,
and two have gone to vertex 2, since the edge from 1 to 2 has weight 2.
Vertex 3 in the new configuration is now unstable. The Sage code for this
example looks like this:
Create the sandpile:
sage: load sandpile.sage
sage: g = {'sink':{},
1:{'sink':1, 2:1, 3:2},
2:{1:1, 3:1},
3:{1:1, 2:1}}
sage: S = Sandpile(g, 'sink')
sage: S.show(edge_labels=true) # to display the graph
Create the configuration:
sage: c = {1:5, 2:0, 3:1}
sage: S.out_degree()
{1: 4, 2: 2, 3: 2, 'sink': 0}
Fire vertex one:
sage: S.fire_vertex(1,c)
{1: 1, 2: 1, 3: 3}
sage: c
{1: 1, 2: 1, 3: 3}
Stabilize the rest of the way:
sage: S.stabilize(c)
[{1: 2, 2: 1, 3: 1}, {1: 1, 2: 2, 3: 3}]
Since vertex 3 has become unstable, it can be fired, which causes vertex 2
to become unstable, etc. Since there is a global sink, repeated firings
eventually lead to a stable configuration. The last line of the Sage code,
above, is a list, the first element of which is the resulting stable
configuration, 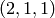 . (The second component records how many times
each vertex fired in the stabilization.)
. (The second component records how many times
each vertex fired in the stabilization.)
Since here is a global sink, every configuration will stabilize after a finite number of vertex-firings. It is not obvious, but the resulting stabilization is independent of the order in which unstable vertices are fired. Thus, each configuration stabilizes to a unique stable configuration.
Laplacian¶
Fix an order on the vertices of  . The Laplacian of
. The Laplacian of  is
is
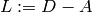
where 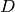 is the diagonal matrix of out-degrees of the vertices and
is the diagonal matrix of out-degrees of the vertices and 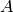 is the
adjacency matrix whose
is the
adjacency matrix whose 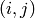 -th entry is the weight of the edge from vertex
-th entry is the weight of the edge from vertex
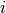 to vertex
to vertex 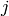 , which we take to be
, which we take to be 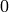 if there is no edge. The reduced
Laplacian,
if there is no edge. The reduced
Laplacian, 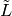 , is the submatrix of the Laplacian formed by removing the row and
column corresponding to the sink vertex. Firing a vertex of a configuration is the same as subtracting the row of the reduced Laplacian.
, is the submatrix of the Laplacian formed by removing the row and
column corresponding to the sink vertex. Firing a vertex of a configuration is the same as subtracting the row of the reduced Laplacian.
Example. (Continued.)
sage: S.vertices() # here is the ordering of the vertices
[1, 2, 3, 'sink']
sage: S.laplacian()
[ 4 -1 -2 -1]
[-1 2 -1 0]
[-1 -1 2 0]
[ 0 0 0 0]
sage: S.reduced_laplacian()
[ 4 -1 -2]
[-1 2 -1]
[-1 -1 2]
The configuration we considered previously:
sage: c = S.list_to_config([5,0,1])
sage: c
{1: 5, 2: 0, 3: 1}
Firing vertex 1 is the same as substracting the
corresponding row from the reduced Laplacian:
sage: S.fire_vertex(1,c)
{1: 1, 2: 1, 3: 3}
sage: S.reduced_laplacian()[0]
(4, -1, -2)
sage: vector([5,0,1]) - vector([4,-1,-2])
(1, 1, 3)
Recurrent elements¶
Imagine an experiment in which grains of sand are dropped one-at-a-time onto a graph, pausing to allow the configuration to stabilize between drops. Some configurations will only be seen once in this process. For example, for most graphs, once sand is dropped on the graph, no addition of sand+stabilization will result in a graph empty of sand. Other configurations—the so-called recurrent configurations—will be seen infinitely often as the process is repeated indefinitely.
To be precise, a configuration  is recurrent if (i) it is stable, and (ii)
given any configuration
is recurrent if (i) it is stable, and (ii)
given any configuration  , there is a configuration
, there is a configuration 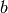 such that
such that
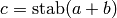 , the stabilization of
, the stabilization of 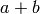 .
.
The maximal-stable configuration, denoted 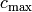 is defined by
is defined by
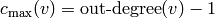 for all nonsink vertices
for all nonsink vertices  . It is clear that
. It is clear that 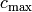 is recurrent. Further, it is not hard to see that a configuration is recurrent if and only if it has the form
is recurrent. Further, it is not hard to see that a configuration is recurrent if and only if it has the form 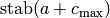 for some configuration
for some configuration  .
.
Example. (Continued.)
sage: S.recurrents(verbose=false)
[[3, 1, 1], [2, 1, 1], [3, 1, 0]]
sage: c = S.list_to_config([2,1,1])
sage: c
{1: 2, 2: 1, 3: 1}
sage: S.is_recurrent(c)
True
sage: S.max_stable()
{1: 3, 2: 1, 3: 1}
Adding any configuration to the max-stable configuration and stabilizing
yields a recurrent configuration.
sage: x = S.list_to_config([1,0,0])
sage: S.add(x,S.max_stable())
{1: 4, 2: 1, 3: 1}
sage: S.stabilize(_)
[{1: 3, 2: 1, 3: 0}, {1: 2, 2: 3, 3: 4}]
sage: c = _[0]
sage: c
{1: 3, 2: 1, 3: 0}
sage: S.is_recurrent(c)
True
Burning Configuration¶
A burning configuration is a nonnegative integer-linear combination of the
rows of the reduced Laplacian matrix having nonnegative entries and such that
every vertex has a path from some vertex in its support. The corresponding
burning script gives the integer-linear combination needed to obtain the
burning configuration. So if 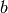 is the burning configuration,
is the burning configuration, 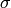 is its
script, and
is its
script, and 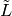 is the reduced Laplacian, then
is the reduced Laplacian, then 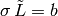 .
The minimal burning configuration is the one with the minimal script (its
components are no larger than the components of any other script for a burning
configuration).
.
The minimal burning configuration is the one with the minimal script (its
components are no larger than the components of any other script for a burning
configuration).
The following are equivalent for a configuration  with burning
configuration
with burning
configuration 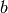 having script
having script 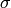 :
:
is recurrent;
stabilizes to
;
- the firing vector for the stabilization of
is
.
The burning configuration and script are computed using a modified version of Speer’s script algorithm. This is a generalization to directed multigraphs of Dhar’s burning algorithm.
Example.
sage: g = {0:{},1:{0:1,3:1,4:1},2:{0:1,3:1,5:1},
3:{2:1,5:1},4:{1:1,3:1},5:{2:1,3:1}}
sage: G = Sandpile(g,0)
sage: G.burning_config()
{1: 2, 2: 0, 3: 1, 4: 1, 5: 0}
sage: G.burning_config().values()
[2, 0, 1, 1, 0]
sage: G.burning_script()
{1: 1, 2: 3, 3: 5, 4: 1, 5: 4}
sage: G.burning_script().values()
[1, 3, 5, 1, 4]
sage: matrix(G.burning_script().values())*G.reduced_laplacian()
[2 0 1 1 0]
Sandpile group¶
The collection of stable configurations forms a commutative monoid with addition defined as ordinary addition followed by stabilization. The identity element is the all-zero configuration. This monoid is a group exactly when the underlying graph is a DAG (directed acyclic graph).
The recurrent elements form a submonoid which turns out to be a group. This
group is called the sandpile group for 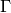 , denoted
, denoted 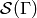 . Its identity element is
usually not the all-zero configuration (again, only in the case that
. Its identity element is
usually not the all-zero configuration (again, only in the case that 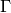 is a DAG). So find the identity element is an interesting question.
is a DAG). So find the identity element is an interesting question.
Let 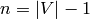 and fix an ordering of the nonsink vertices. Let
and fix an ordering of the nonsink vertices. Let 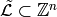 denote the
column-span of
denote the
column-span of 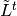 , the tranpose of the reduced Laplacian. It
is a theorem that
, the tranpose of the reduced Laplacian. It
is a theorem that
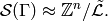
Thus, the number of element of the sandpile group is 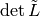 , which by the
matrix-tree theorem is the number of weighted trees directed into the sink.
, which by the
matrix-tree theorem is the number of weighted trees directed into the sink.
Example. (Continued.)
sage: S.group_order()
3
sage: S.elementary_divisors()
[1, 1, 3]
sage: S.reduced_laplacian().dense_matrix().smith_form()
([1 0 0]
[0 1 0]
[0 0 3],
[ 0 0 1]
[ 1 0 0]
[ 0 1 -1],
[3 1 4]
[4 1 6]
[4 1 5])
Adding the identity to any recurrent configuration and stabilizing yields
the same recurrent configuration:
sage: S.identity()
{1: 3, 2: 1, 3: 0}
sage: i = S.identity()
sage: m = S.max_stable()
sage: S.stably_add(i,m)[0] == m
True
Self-organized criticality¶
The sandpile model was introduced by Bak, Tang, and Wiesenfeld in the paper,
Self-organized criticality: an explanation of 1/ƒ noise [BTW]. The term
self-organized criticality has no generally accepted definition, but can be
loosely taken to mean like the sandpile model on a grid-graph. The grid
graph is just a grid with an extra sink vertex. The vertices on the interior
of each side have one edge to the sink, and the corner vertices have an edge of
weight 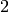 . Thus, every nonsink vertex has out-degree
. Thus, every nonsink vertex has out-degree 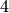 .
.
One property that is taken as characteristic of self-organized criticality is the presence of a power law (by which is meant an exponential law) describing the behavior of some ascpect of the system. For the grid graph, computer experiments—I do not think there is a proof, yet—indicate that the distribution of avalanche sizes obeys a power law. In the example below, the size of an avalanche is taken to be the sum of the number of imes each vertex fires.
Example.
Distribution of avalanche sizes:
sage: S = Sandpile(grid(10,10),'sink')
sage: S.set_config(S.max_stable())
sage: a = [sum(S.stabilize(S.add_random())[1].values()) for i in range(10000)]
sage: p = list_plot([[log(i+1),log(a.count(i))] for i in [0..max(a)] if a.count(i)])
sage: p.axes_labels(['N','D(N)'])
sage: p
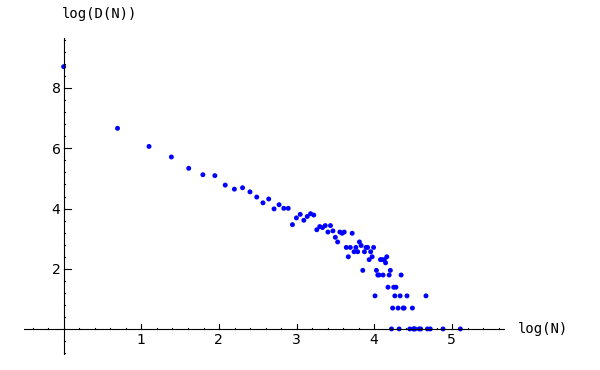
Distribution of avalanche sizes
Discrete Riemann surfaces¶
A reference for this section is Riemann-Roch and Abel-Jacobi theory on a finite graph [BN].
A divisor on 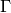 is an element of the free abelian group on its vertices,
including the sink. Suppose, as above, that the
is an element of the free abelian group on its vertices,
including the sink. Suppose, as above, that the 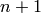 vertices of
vertices of 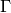 have
been ordered, and that
have
been ordered, and that 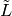 is the column span of the transpose of the
Laplacian. A divisor is then identified with an element
is the column span of the transpose of the
Laplacian. A divisor is then identified with an element 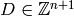 .
Two divisors are linearly equivalent if they differ by an element of
.
Two divisors are linearly equivalent if they differ by an element of
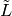 . A divisor
. A divisor 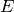 is effective, written
is effective, written 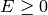 , if
, if 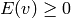 for
each
for
each 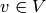 , i.e., if
, i.e., if 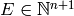 . The degree of a divisor,
. The degree of a divisor, 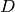 ,
is
,
is 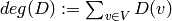 . The divisors of degree zero modulo linear
equivalence form the Picard group, or Jacobian of the graph. For an
undirected graph, the Picard group is isomorphic to the sandpile group.
. The divisors of degree zero modulo linear
equivalence form the Picard group, or Jacobian of the graph. For an
undirected graph, the Picard group is isomorphic to the sandpile group.
The complete linear system for a divisor 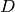 , denoted
, denoted 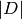 , is the collection
of effective divisors linearly equivalent to
, is the collection
of effective divisors linearly equivalent to 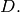 To describe the Riemann-Roch
theorem in this context, suppose that
To describe the Riemann-Roch
theorem in this context, suppose that 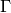 is
an undirected, unweighted graph. The dimension,
is
an undirected, unweighted graph. The dimension, 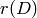 of
the linear system
of
the linear system 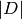 is
is 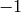 if
if 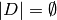 and otherwise is the greatest
integer
and otherwise is the greatest
integer  such that
such that 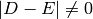 for all effective divisors
for all effective divisors 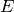 of degree
of degree  .
Define the canonical divisor by
.
Define the canonical divisor by 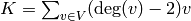 and the genus
by
and the genus
by 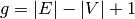 . The
Riemann-Roch theorem says that for any divisor
. The
Riemann-Roch theorem says that for any divisor 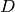 ,
,
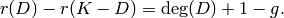
Example. Some of the following calculations require the installation of 4ti2.
The sandpile on the complete graph on 5 vertices:
sage: Gamma = graphs.CompleteGraph(5)
sage: S = Sandpile(Gamma,0)
The num_edges method counts each undirected edge twice:
sage: g = S.num_edges()/2 - S.num_verts() + 1
A divisor on the graph:
sage: D = S.list_to_div([1,2,2,0,2])
Verify the Riemann-Roch theorem:
sage: degD = sum(D.values())
sage: K = S.all_k_div(2)
sage: F = S.subtract(K,D)
sage: r_of_D = S.r_of_D(D)[0]
0
1
2
sage: r_of_F = S.r_of_D(F)[0]
0
sage: r_of_D - r_of_F == degD + 1 - g
True
The effective divisors linearly equivalent to D:
sage: S.effective_div(D)
[{0: 0, 1: 1, 2: 1, 3: 4, 4: 1},
{0: 4, 1: 0, 2: 0, 3: 3, 4: 0},
{0: 1, 1: 2, 2: 2, 3: 0, 4: 2}]
Algebraic geometry of sandpiles¶
A reference for the following material is in the works [PP].
Affine¶
Let 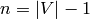 , and fix an ordering on the nonsink vertices of
, and fix an ordering on the nonsink vertices of 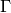 . let
. let
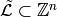 denote the column-span of
denote the column-span of
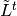 , the tranpose of the reduced Laplacian. Label vertex
, the tranpose of the reduced Laplacian. Label vertex 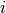 with the
indeterminate
with the
indeterminate 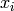 , and let
, and let ![\mathbb{C}[\Gamma_s] = \mathbb{C}[x_1,\dots,x_n]](_images/math/e1ef1ba99ea450324dab0463f91ec0e0ad5e59cc.png) .
(Here,
.
(Here,  denotes the sink vertex of
denotes the sink vertex of 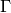 .) The sandpile ideal or
toppling ideal is the lattice ideal for
.) The sandpile ideal or
toppling ideal is the lattice ideal for 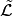 :
:
![I = I(\Gamma_s) := \{x^u-x^v: u-v
\tilde{\mathcal{L}}\}\subset\mathbb{C}[\Gamma_s],](_images/math/a010172ee0635f64f09b73ef0a2b561f46221073.png)
where 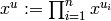 for
for 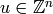 .
.
For each 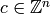 define
define 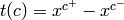 where
where
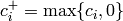 and
and 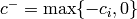 so that
so that 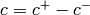 .
Then, for each
.
Then, for each 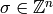 , define
, define 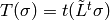 . It then turns out that
. It then turns out that
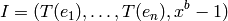
where 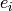 is the
is the 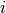 -th standard basis vector and
-th standard basis vector and 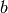 is any burning
configuration.
is any burning
configuration.
The affine coordinate ring, ![\mathbb{C}[\Gamma_s]/I,](_images/math/c86f192525ebd188ad7eba9f1677c8078a919e95.png) is isomorphic to the group
algebra of the sandpile group,
is isomorphic to the group
algebra of the sandpile group, ![\mathbb{C}[\mathcal{S}(\Gamma)].](_images/math/56f2228438171b93edb6630402ebc5382f18caf9.png)
The standard term-ordering on ![\mathbb{C}[\Gamma_s]](_images/math/3137ebe0914960c96f1bf4ced19fd81ae0d8b321.png) is graded reverse
lexigraphical order with
is graded reverse
lexigraphical order with 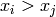 if vertex
if vertex 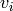 is further from the sink than
vertex
is further from the sink than
vertex 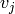 . If
. If 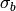 is the script for a burning configuration (not
necessarily minimal), then
is the script for a burning configuration (not
necessarily minimal), then
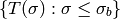
is a Groebner basis for 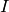 .
.
Projective¶
Now let ![\mathbb{C}[\Gamma]=\mathbb{C}[x_0,x_1,\dots,x_n]](_images/math/89b6b44feba8cbf1687365cfbcaff81331aff2f4.png) , where
, where 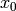 corresponds to the sink vertex. The homogeneous sandpile ideal, denoted
corresponds to the sink vertex. The homogeneous sandpile ideal, denoted
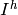 , is obtaining by homogenizing
, is obtaining by homogenizing 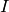 with respect to
with respect to 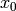 . Let
. Let 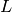 be the
(full) Laplacian, and
be the
(full) Laplacian, and 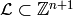 be the column span of
its transpose,
be the column span of
its transpose, 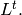 Then
Then 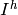 is the lattice ideal for
is the lattice ideal for 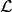 :
:
![I^h = I^h(\Gamma) := \{x^u-x^v: u-v \in\mathcal{L}\}\subset\mathbb{C}[\Gamma].](_images/math/efc956d162e507dd37203fc62f377ccd0e66e311.png)
This ideal can be calculated by saturating the ideal
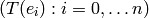
with respect to the product of the indeterminates: 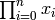 (extending
the
(extending
the 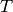 operator in the obvious way). A Groebner basis with respect to the
degree lexicographic order describe above (with
operator in the obvious way). A Groebner basis with respect to the
degree lexicographic order describe above (with 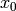 the smallest vertex), is
obtained by homogenizing each element of the Groebner basis for the
non-homogeneous sandpile ideal with respect to
the smallest vertex), is
obtained by homogenizing each element of the Groebner basis for the
non-homogeneous sandpile ideal with respect to 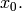
Example.
sage: g = {0:{},1:{0:1,3:1,4:1},2:{0:1,3:1,5:1},
3:{2:1,5:1},4:{1:1,3:1},5:{2:1,3:1}}
sage: S = Sandpile(g, 0)
sage: S.ring()
// characteristic : 0
// number of vars : 6
// block 1 : ordering dp
// : names x_5 x_4 x_3 x_2 x_1 x_0
// block 2 : ordering C
The homogeneous sandpile ideal:
sage: S.ideal()
x_2-x_0,
x_3^2-x_5*x_0,
x_5*x_3-x_0^2,
x_4^2-x_3*x_1,
x_5^2-x_3*x_0,
x_1^3-x_4*x_3*x_0,
x_4*x_1^2-x_5*x_0^2
its resolution:
sage: S.resolution()
'R <-- R^7 <-- R^19 <-- R^25 <-- R^16 <-- R^4'
and Betti table:
sage: S.betti()
0 1 2 3 4 5
------------------------------------------
0: 1 1 - - - -
1: - 4 6 2 - -
2: - 2 7 7 2 -
3: - - 6 16 14 4
------------------------------------------
total: 1 7 19 25 16 4
The Hilbert function:
sage: S.hilbert_function()
[1, 5, 11, 15]
and its first differences (which counts the number of superstable
configurations in each degree):
sage: S.first_diffs_hilb()
[1, 4, 6, 4]
sage: x = [sum(i) for i in S.superstables(False)]
sage: sorted(x)
[0, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 3, 3, 3, 3]
The degree in which the Hilbert function equals the Hilbert polynomial, the
latter always being a constant in the case of a sandpile ideal:
sage: S.postulation()
3
Zeros¶
The zero set for the sandpile ideal 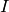 is
is
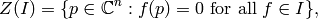
the set of simultaneous zeros of the polynomials in 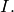 Letting
Letting 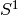 denote
the unit circle in the complex plane,
denote
the unit circle in the complex plane, 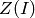 is a finite
subgroup of
is a finite
subgroup of 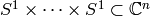 , isomorphic to the
sandpile group. The zero set is actually linearly isomorphic to a faithful representation of the sandpile group on
, isomorphic to the
sandpile group. The zero set is actually linearly isomorphic to a faithful representation of the sandpile group on 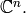
Example. (Continued.)
sage: S = Sandpile({0: {}, 1: {2: 2}, 2: {0: 4, 1: 1}}, 0)
sage: S.ideal()
x_1^2-x_2^2,
x_1*x_2^3-x_0^4,
x_2^5-x_1*x_0^4
Approximation to the zero set (setting ``x_0 = 1``):
sage: S.solve()
[[0.707107*I - 0.707107, 0.707107 - 0.707107*I],
[-0.707107*I - 0.707107, 0.707107*I + 0.707107],
[-1*I, -1*I],
[I, I],
[0.707107*I + 0.707107, -0.707107*I - 0.707107],
[0.707107 - 0.707107*I, 0.707107*I - 0.707107],
[1, 1],
[-1, -1]]
sage: len(_) == S.group_order()
True
The zeros are generated as a group by a single vector:
sage: S.points()
[[e^(1/4*I*pi), e^(-3/4*I*pi)]]
Resolutions¶
The homogeneous sandpile ideal, 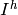 , has a free resolution graded by the
divisors on
, has a free resolution graded by the
divisors on 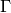 modulo linear equivalence. (See the section on
Discrete Riemann Surfaces for the language of
divisors and linear equivalence.) Let
modulo linear equivalence. (See the section on
Discrete Riemann Surfaces for the language of
divisors and linear equivalence.) Let
![S=\mathbb{C}[\Gamma]=\mathbb{C}[x_0,\dots,x_n]](_images/math/2cb933567163075ccbd51b470c14654e26fc0b71.png) , as above, and let
, as above, and let
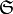 denote the group of divisors modulo rational equivalence. Then
denote the group of divisors modulo rational equivalence. Then
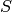 is graded by
is graded by 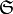 by letting
by letting 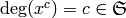 for
each monomial
for
each monomial 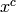 . The minimal free resolution of
. The minimal free resolution of 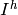 has the form
has the form
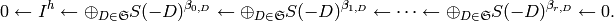
where the 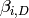 are the Betti numbers for
are the Betti numbers for 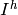 .
.
For each divisor class 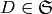 , define a simplicial complex,
, define a simplicial complex,
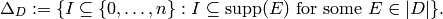
The Betti number 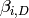 equals the dimension over
equals the dimension over 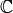 of the
of the
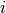 -th reduced homology group of
-th reduced homology group of 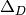 :
:
sage: S = Sandpile({0:{},1:{0: 1, 2: 1, 3: 4},2:{3: 5},3:{1: 1, 2: 1}},0)
Representatives of all divisor classes with nontrivial homology:
sage: p = S.betti_complexes()
sage: p[0]
[{0: -8, 1: 5, 2: 4, 3: 1},
Simplicial complex with vertex set (0, 1, 2, 3) and facets {(1, 2), (3,)}]
The homology associated with the first divisor in the list:
sage: D = p[0][0]
sage: S.effective_div(D)
[{0: 0, 1: 1, 2: 1, 3: 0}, {0: 0, 1: 0, 2: 0, 3: 2}]
sage: [S.support(E) for E in S.effective_div(D)]
[[1, 2], [3]]
sage: S.Dcomplex(D)
Simplicial complex with vertex set (0, 1, 2, 3) and facets {(1, 2), (3,)}
sage: S.Dcomplex(D).homology()
{0: Z, 1: 0}
The minimal free resolution:
sage: S.resolution()
'R <-- R^5 <-- R^5 <-- R^1'
sage: S.betti()
0 1 2 3
------------------------------
0: 1 - - -
1: - 5 5 -
2: - - - 1
------------------------------
total: 1 5 5 1
sage: len(p)
11
The degrees and ranks of the homology groups foreach element of the list p (compare with the
Betti table, above):
sage: [[sum(d[0].values()),d[1].betti()] for d in p]
[[2, {0: 1, 1: 0}],
[3, {0: 0, 1: 1, 2: 0}],
[2, {0: 1, 1: 0}],
[3, {0: 0, 1: 1, 2: 0}],
[2, {0: 1, 1: 0}],
[3, {0: 0, 1: 1, 2: 0}],
[2, {0: 1, 1: 0}],
[3, {0: 0, 1: 1}],
[2, {0: 1, 1: 0}],
[3, {0: 0, 1: 1, 2: 0}],
[5, {0: 0, 1: 0, 2: 1}]]
Installation¶
It is assumed that Sage is already installed. If not, please see the main Sage homepage for installation instructions. To use sandpile.sage:
- download sandpile.sage
- start Sage, and issue the command
sage: load sandpile.sage
You may need to give the full path name to sandpile.sage.
Warning
The methods for computing linear systems of divisors and their corresponding simplicial complexes require the installation of 4ti2.
To make 4ti2 usable from Sage Sandpiles:
- download the program from the 4ti2 homepage, and follow the installation instructions given there
- open sandpiles.sage in your favorite text editor and edit the following line (near the beginning of the file, near the copyright statement and the start of the definition of the Sandpile class), replacing the path_to_zsolve string with the path to the executables in your 4ti2 directory:
# set the following if 4ti2 is installed
path_to_zsolve = '/home/davidp/math/sandpile/4ti2/linux_x86/'
- start Sage and load sandpiles.sage as described above.
Usage¶
Initialization¶
Most of sandpile.sage consists of the definition of the class
Sandpile representing the abelian sandpile model on a graph  .
Initialization has the form
.
Initialization has the form
sage: S = Sandpile(graph, sink)
where graph represents a graph and sink is the key for the sink vertex. There are four possible forms for graph:
- a Python dictionary of dictionaries:
sage: g = {0: {}, 1: {0: 1, 3: 1, 4: 1}, 2: {0: 1, 3: 1, 5: 1},
3: {2: 1, 5: 1}, 4: {1: 1, 3: 1}, 5: {2: 1, 3: 1}}
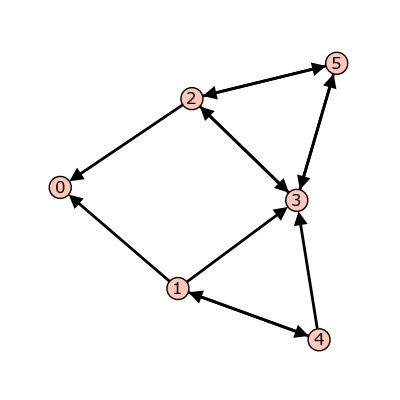
Graph from dictionary of dictionaries.
Each key is the name of a vertex. Next to each vertex name  is a dictionary
consisting of pairs: vertex: weight. Each pair represents a directed edge
emanating from
is a dictionary
consisting of pairs: vertex: weight. Each pair represents a directed edge
emanating from  and ending at vertex having (non-negative integer) weight
equal to weight. Loops are allowed. In the example above, all of the weights are 1.
and ending at vertex having (non-negative integer) weight
equal to weight. Loops are allowed. In the example above, all of the weights are 1.
- a Python dictionary of lists:
sage: g = {0: [], 1: [0, 3, 4], 2: [0, 3, 5],
3: [2, 5], 4: [1, 3], 5: [2, 3]}
This is a short-hand when all of the edge-weights are equal to 1. The above example is for the same displayed graph.
- a Sage graph (of type sage.graphs.graph.Graph):
sage: g = graphs.CompleteGraph(5)
sage: S = Sandpile(g, 0)
sage: type(g)
<class 'sage.graphs.graph.Graph'>
- a Sage digraph:
sage: S = Sandpile(digraphs.RandomDirectedGNC(6), 0)
sage: S.show()
A random graph.
See http://sagemath.org/doc/reference/sage/graphs/graph_generators.html for more information on the Sage graph library and graph constructors.
Each of these four formats is preprocessed by the Sandpile class so that, internally, the graph is represented by the dictionary of dictionaries format first presented. This internal format is returned by dict():
sage: S = Sandpile({0:[], 1:[0, 3, 4], 2:[0, 3, 5],
3: [2, 5], 4: [1, 3], 5: [2, 3]},0)
sage: S.dict()
{0: {},
1: {0: 1, 3: 1, 4: 1},
2: {0: 1, 3: 1, 5: 1},
3: {2: 1, 5: 1},
4: {1: 1, 3: 1},
5: {2: 1, 3: 1}}
Note
The user is responsible for assuring that each vertex has a directed path into the designated sink. If the sink has out-edges, these will be ignored for the purposes of sandpile calculations (but not calculations on divisors).
Code for checking whether a given vertex is a sink:
sage: S = Sandpile({0:[], 1:[0, 3, 4], 2:[0, 3, 5],
3: [2, 5], 4: [1, 3], 5: [2, 3]},0)
sage: [S.distance(v,0) for v in S.vertices()] # 0 is a sink
[0, 1, 1, 2, 2, 2]
sage: [S.distance(v,1) for v in S.vertices()] # 1 is not a sink
[+Infinity, 0, +Infinity, +Infinity, 1, +Infinity]
Methods¶
Here is a summary of Sandpile methods. The summary is followed by a list of complete descriptions of these methods. There are many more methods available for a Sandpile, e.g., those inherited from the class DiGraph. To see them all, enter
sage: dir(Sandpile)
Summary of methods.
- add(c, d) — The sum of c and d without stabilizing.
- add_random(config) — Add a random grain of sand to config.
- all_k_config(k) — The configuration having k grains of sand on each vertex.
- all_k_div(k) — The divisor having k grains of sand on each vertex.
- betti(verbose) — The Betti table for the homogeneous sandpile ideal.
- betti_complexes() — All simplicial complexes arising from divisors having nontrivial homology.
- burning_config() — A minimal burning configuration.
- burning_script() — A script for the minimal burning configuration.
- compare_configs(c, d) — Is c at least as large as d at each vertex?
- config() — The current saved configuration.
- config_to_list(config) — Convert a configuration into a list.
- Dcomplex(D) — The simplicial complex determined by the supports of effective divisors linearly equivalent to D.
- dict() — Returns a dictionary of dictionaries representing a directed graph.
- div_to_list(div) — Convert a divisor into a list in the order determined by vertices().
- dualize(config) — Returns max_stable - config.
- effective_div(div) — Returns all effective
divisors linearly equivalent to
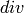 .
. - element_order(config) — Returns the order of the recurrent element equivalent to config.
- elementary_divisors() — The elementary divisors of the sandpile group.
- equivalent_recurrent(config) — The recurrent configuration equivalent to the given configuration (+ firing vector).
- equivalent_superstable(config) — The superstable configuration equivalent to the given configuration (+ firing vector).
- fire_vertex(v, config) — Fire (topple) a given vertex of a configuration.
- first_diffs_hilb() — The first differences of the Hilbert function of the homogeneous sandpile ideal.
- groebner() — A Groebner basis for the homogeneous sandpile ideal with respect to the standard sandpile ordering (see ring).
- group_order() — The size of the sandpile group.
- hilbert_function() — The Hilbert function of the homogeneous sandpile ideal.
- ideal() — The saturated, homogeneous sandpile ideal.
- identity() — The identity configuration.
- in_degree(v) — The in-degree of a vertex or a list of all in-degrees.
- is_recurrent(config) Is config is recurrent, i.e., an element of the sandpile group?
- is_stable(config) — Is config stable?
- is_superstable(config) — Is config superstable, i.e., does it not permit multiset firings?
- is_symmetric(c, orbits) — Is
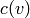 is constant over the vertices in each sublist of orbits?
is constant over the vertices in each sublist of orbits? - laplacian() — The Laplacian matrix of the graph.
- linear_system(div) — The complete linear system of a divisor.
- list_to_config(L) — Convert a list into a configuration.
- list_to_div(L) — Convert a list of integers into a divisor.
- max_stable() — The maximal stable configuration.
- nonsink_vertices() — The names of the nonsink vertices.
- out_degree(v) — The out-degree of a vertex or a list of all out-degrees.
- points() — Generators for the multiplicative group of zeros of the sandpile ideal.
- postulation() — The postulation number of the sandpile ideal.
- r_of_D(D) — Computes r(D) and an effective divisor F such that |D - F| is empty.
- recurrent_difference(config1, config2) — A recurrent configuration equivalent to the config1 - config2.
- recurrents(verbose) — The list of recurrent configurations.
- reduced_laplacian() — The reduced Laplacian matrix of the graph.
- reset_config(config) — Turn config into the zero configuration.
- resolution(verbose) — The minimal free resolution of the homogeneous sandpile ideal.
- ring() — The ring containing the homogeneous sandpile ideal.
- set_config(config) — Sets the current configuration to config.
- sink() — The identifier for the sink vertex.
- solve() — Computes approximations of the complex affine zeros of the sandpile ideal.
- stabilize(config) — The stabilized configuration and its firing vector.
- stabilize_one_step(config) — Fire each unstable vertex in config (+ firing vector).
- stably_add(config1, config2) — The stabilization of the sum of two configurations (+ firing vector).
- subtract(c, d) — The difference of c - d of configurations or divisors.
- superstables(verbose) — The superstable configurations (
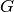 -parking functions).
-parking functions). - support(D) — The list of keys of nonzero values of the dictionary D.
- symmetric_recurrents(orbits) — The list of symmetric recurrent configurations.
- unsaturated_ideal() — The unsaturated, homogeneous sandpile ideal.
- unstable(config) — The list of unstable vertices in config.
- version() — The version number of Sage Sandpiles.
- vertices() — A list of the vertices.
Complete descriptions of methods.
add(c, d)
Returns the sum of c and d without stabilizing.
INPUT:
c, d - dict (configurations or divisors)
OUTPUT:
dict (configuration or divisor)
EXAMPLES:
Adding configurations:
sage: S = sandlib('generic') sage: m = S.max_stable() sage: m {1: 2, 2: 2, 3: 1, 4: 1, 5: 1} sage: S.add(m, m) {1: 4, 2: 4, 3: 2, 4: 2, 5: 2}Adding divisors:
sage: D = S.list_to_div([1,-3,2,0,4,-2]) sage: E = S.list_to_div([2, 3,4,1,1,-2]) sage: S.add(D,E) {0: 3, 1: 0, 2: 6, 3: 1, 4: 5, 5: -4}
—
add_random(config=None)
Add one grain of sand to a random nonsink vertex. The config argument can be a configuration or a divisor.
INPUT:
config (optional) - dict (a configuration or divisor)
OUTPUT:
None
EXAMPLES:
We compute the ‘sizes’ of the avalanches caused by adding random grains of sand to the maximal stable configuration on a grid graph. The function stabilize() returns the firing vector of the stabilization, a dictionary whose values say how many times each vertex fires in the stabilization.
sage: S = Sandpile(grid(4,4),'sink') sage: a = [sum(S.stabilize(S.add_random())[1].values()) for i in range(1000)] sage: b = [[log(i+1),log(a.count(i))] for i in [0..max(a)] if a.count(i)] sage: list_plot(b)Also works for divisors:
sage: S = sandlib('generic') sage: D = S.list_to_div([0,0,0,0,0,0]) sage: S.add_random(D) sage: D #random {0: 0, 1: 0, 2: 0, 3: 0, 4: 0, 5: 1}
—
all_k_config(k)
The configuration having k grains of sand on each vertex.
INPUT:
k - integer
OUTPUT:
dict (configuration)
EXAMPLES:
sage: S = sandlib('generic') sage: S.all_k_config(7) {1: 7, 2: 7, 3: 7, 4: 7, 5: 7}
—
all_k_div(k)
The divisor having k grains of sand on each vertex.
INPUT:
k - integer
OUTPUT:
dict (divisor)
EXAMPLES:
sage: S = sandlib('generic') sage: S.all_k_div(7) {0: 7, 1: 7, 2: 7, 3: 7, 4: 7, 5: 7}
—
betti(verbose=True)
Computes the Betti table for the homogeneous sandpile ideal. If verbose is True, it prints the standard Betti table, otherwise, it returns a less formated table.
INPUT:
verbose (optional) - boolean
OUTPUT:
Betti numbers for the sandpile
EXAMPLE:
sage: S = sandlib('generic') sage: S.betti() 0 1 2 3 4 5 ------------------------------------------ 0: 1 1 - - - - 1: - 4 6 2 - - 2: - 2 7 7 2 - 3: - - 6 16 14 4 ------------------------------------------ total: 1 7 19 25 16 4
—
betti_complexes()
Returns a list of all the divisors with nonempty linear systems whose corresponding simplicial complexes have nonzero homology in some dimension. Each such divisors is returned with its corresponding simplicial complex.
INPUT:
None
OUTPUT:
list (of pairs [divisors, corresponding simplicial complex])
EXAMPLES:
sage: S = Sandpile({0:{},1:{0: 1, 2: 1, 3: 4},2:{3: 5},3:{1: 1, 2: 1}},0) sage: p = S.betti_complexes() sage: p[0] [{0: -8, 1: 5, 2: 4, 3: 1}, Simplicial complex with vertex set (0, 1, 2, 3) and facets {(1, 2), (3,)}] sage: S.resolution() 'R <-- R^5 <-- R^5 <-- R^1' sage: S.betti() 0 1 2 3 ------------------------------ 0: 1 - - - 1: - 5 5 - 2: - - - 1 ------------------------------ total: 1 5 5 1 sage: len(p) 11
—
burning_config()
A minimal burning configuration.
INPUT:
None
OUTPUT:
dict (configuration)
EXAMPLES:
sage: g = {0:{},1:{0:1,3:1,4:1},2:{0:1,3:1,5:1}, 3:{2:1,5:1},4:{1:1,3:1},5:{2:1,3:1}} sage: G = Sandpile(g,0) sage: G.burning_config() {1: 2, 2: 0, 3: 1, 4: 1, 5: 0} sage: G.config_to_list(G.burning_config()) [2, 0, 1, 1, 0] sage: G.burning_script() {1: 1, 2: 3, 3: 5, 4: 1, 5: 4} sage: script = G.config_to_list(G.burning_script()) sage: script [1, 3, 5, 1, 4] sage: matrix(script)*G.reduced_laplacian() [2 0 1 1 0]NOTES:
The burning configuration and script are computed using a modified version of Speer’s script algorithm. This is a generalization to directed multigraphs of Dhar’s burning algorithm.
A burning configuration is a nonnegative integer-linear combination of the rows of the reduced Laplacian matrix having nonnegative entries and such that every vertex has a path from some vertex in its support. The corresponding burning script gives the integer-linear combination needed to obtain the burning configuration. So if
is the burning configuration,
is its script, and
is the reduced Laplacian, then
. The minimal burning configuration is the one with the minimal script (its components are no larger than the components of any other script for a burning configuration).
The following are equivalent for a configuration
with burning configuration
having script
:
is recurrent;
stabilizes to
;
- the firing vector for the stabilization of
is
.
—
burning_script()
A script for the minimal burning configuration.
INPUT:
None
OUTPUT:
dict
EXAMPLES:
sage: g = {0:{},1:{0:1,3:1,4:1},2:{0:1,3:1,5:1}, 3:{2:1,5:1},4:{1:1,3:1},5:{2:1,3:1}} sage: G = Sandpile(g,0) sage: G.burning_config() {1: 2, 2: 0, 3: 1, 4: 1, 5: 0} sage: G.config_to_list(G.burning_config()) [2, 0, 1, 1, 0] sage: G.burning_script() {1: 1, 2: 3, 3: 5, 4: 1, 5: 4} sage: script = G.config_to_list(G.burning_script()) sage: script [1, 3, 5, 1, 4] sage: matrix(script)*G.reduced_laplacian() [2 0 1 1 0]NOTES:
The burning configuration and script are computed using a modified version of Speer’s script algorithm. This is a generalization to directed multigraphs of Dhar’s burning algorithm.
A burning configuration is a nonnegative integer-linear combination of the rows of the reduced Laplacian matrix having nonnegative entries and such that every vertex has a path from some vertex in its support. The corresponding burning script gives the integer-linear combination needed to obtain the burning configuration. So if
is the burning configuration,
is its script, and
is the reduced Laplacian, then
. The minimal burning configuration is the one with the minimal script (its components are no larger than the components of any other script for a burning configuration).
The following are equivalent for a configuration
with burning configuration
having script
:
is recurrent;
stabilizes to
;
- the firing vector for the stabilization of
is
.
—
compare_configs(c, d)
Returns True if each c is at least as large as d at each vertex.
INPUT:
c, d - dict (configurations or divisors)
OUTPUT:
boolean
EXAMPLES:
sage: S = sandlib('generic') sage: c = S.all_k_config(5) sage: d = S.all_k_config(4) sage: S.compare_configs(c,d) True sage: S.compare_configs(d,c) False
—
config()
The current saved configuration.
INPUT:
None
OUTPUT:
None
EXAMPLES:
sage: G = sandlib('generic') sage: G.set_config(G.max_stable()) sage: G.config() == G.max_stable() True sage: G.add(G.max_stable(),G.identity()) {1: 4, 2: 4, 3: 2, 4: 2, 5: 1} sage: G.config() {1: 4, 2: 4, 3: 2, 4: 2, 5: 1}NOTES:
Each sandpile has a saved configuration (initially the zero configuration) The configuration can be set with the set_config() method and may be affected by certain other methods, e.g., stabilize(), add(), and add_random()—usually those methods that output configurations.
—
config_to_list(config)
Convert a configuration into a list in the order determined by nonsink_vertices().
INPUT:
config - dict (configuration)
OUTPUT:
list of integers
EXAMPLES:
sage: S = sandlib('generic') sage: c = S.list_to_config([5,4,3,2,1]) sage: c {1: 5, 2: 4, 3: 3, 4: 2, 5: 1} sage: S.config_to_list(c) [5, 4, 3, 2, 1]NOTES:
The method checks the length of config but not the types of its entries.
—
Dcomplex(D)
Returns the simplicial complex determined by the supports of the effective divisors linearly equivalent to D.
INPUT:
D - dict (divisor)
OUTPUT:
simplicial complex
EXAMPLES:
sage: S = sandlib('generic') sage: p = S.Dcomplex(S.list_to_div([0,1,2,0,0,1])) sage: p.homology() {0: 0, 1: Z x Z, 2: 0, 3: 0} sage: p.f_vector() [1, 6, 15, 9, 1] sage: p.betti() {0: 0, 1: 2, 2: 0, 3: 0}
—
dict()
Returns a dictionary of dictionaries representing a directed graph.
INPUT:
None
OUTPUT:
dict
EXAMPLES:
sage: G = sandlib('generic') sage: G.dict() {0: {}, 1: {0: 1, 3: 1, 4: 1}, 2: {0: 1, 3: 1, 5: 1}, 3: {2: 1, 5: 1}, 4: {1: 1, 3: 1}, 5: {2: 1, 3: 1}} sage: G.sink() 0
—
div_to_list(div)
Convert a divisor into a list in the order determined by vertices().
INPUT:
div - dict (divisor)
OUTPUT:
list of integers
EXAMPLES:
sage: S = sandlib('generic') sage: c = S.list_to_div([6,5,4,3,2,1]) sage: c {0: 6, 1: 5, 2: 4, 3: 3, 4: 2, 5: 1} sage: S.div_to_list(c) [6, 5, 4, 3, 2, 1]NOTES:
The method checks the length of div but not the types of its entries.
—
dualize(config=None)
Returns max_stable - config.
INPUT:
config (optional) - dict (configuration)
OUTPUT:
dict (configuration)
EXAMPLES:
sage: S = sandlib('generic') sage: S.dualize(S.max_stable()) {1: 0, 2: 0, 3: 0, 4: 0, 5: 0}
—
effective_div(div):
Returns all effective divisors linearly equivalent to div.
INPUT:
div - dict (divisor)
OUTPUT:
list (of divisors)
EXAMPLES:
sage: S = sandlib('generic') sage: D = S.list_to_div([0,0,0,0,0,2]) sage: S.effective_div(D) [{0: 1, 1: 0, 2: 0, 3: 1, 4: 0, 5: 0}, {0: 0, 1: 0, 2: 1, 3: 1, 4: 0, 5: 0}, {0: 0, 1: 0, 2: 0, 3: 0, 4: 0, 5: 2}] sage: [S.div_to_list(d) for d in _] [[1, 0, 0, 1, 0, 0], [0, 0, 1, 1, 0, 0], [0, 0, 0, 0, 0, 2]]
—
element_order(config=None)
Returns the order of the recurrent element equivalent to config.
INPUT:
config (optional) - configuration
OUTPUT:
integer
EXAMPLES:
sage: S = sandlib('generic') sage: [S.element_order(r) for r in S.recurrents()] [1, 3, 15, 5, 5, 15, 5, 15, 3, 15, 15, 5, 15, 15, 15]
—
elementary_divisors()
The elementary divisors of the sandpile group (a finite abelian group).
INPUT:
None
OUTPUT:
list of integers
EXAMPLES:
sage: S = sandlib('generic') sage: S.elementary_divisors() [1, 1, 1, 1, 15]
—
equivalent_recurrent(config)
Returns the recurrent configuration equivalent to the given configuration and also returns the corresponding firing vector.
INPUT:
config - dict (configuration)
OUTPUT:
[configuration, firing_vector]
EXAMPLES:
sage: S = sandlib('generic') sage: c = [0,0,0,0,0] sage: config = S.list_to_config([0,0,0,0,0]) sage: x = S.equivalent_recurrent(config) sage: x[0] == S.identity() True sage: r = [x[0][v] for v in S.nonsink_vertices()] sage: f = [x[1][v] for v in S.nonsink_vertices()] sage: vector(r) == vector(c) - vector(f)*S.reduced_laplacian() TrueNOTES:
Let
be the reduced laplacian,
the initial configuration,
the returned configuration, and
the firing vector. Then
.
—
equivalent_superstable(config)
Returns the superstable configuration equivalent to the given configuration and also returns the corresponding firing vector.
INPUT:
config - dict (configuration)
OUTPUT:
[configuration, firing_vector]
EXAMPLES:
sage: S = sandlib('generic') sage: m = S.max_stable() sage: x = S.equivalent_superstable(m) sage: S.is_superstable(x[0]) True sage: s = [x[0][v] for v in S.nonsink_vertices()] sage: f = [x[1][v] for v in S.nonsink_vertices()] sage: m = [m[v] for v in S.nonsink_vertices()] sage: vector(s) == vector(m) - vector(f)*S.reduced_laplacian()NOTES:
Let
be the reduced laplacian,
the initial configuration,
the returned configuration, and
the firing vector. Then
.
—
fire_vertex(v, config=None)
Fire (topple) a given vertex of a configuration.
INPUT:
- v - vertex name
- config - dict
OUTPUT:
dict (configuration)
EXAMPLES:
sage: G = sandlib('generic') sage: c = G.add(G.max_stable(),G.identity()) sage: G.unstable(c) [1, 2, 3, 4] sage: c {1: 4, 2: 4, 3: 2, 4: 2, 5: 1} sage: G.fire_vertex(1,c) {1: 1, 2: 4, 3: 3, 4: 3, 5: 1}NOTES:
This method fires vertex v in config provided v is a nonsink, unstable vertex. Returns the result (and modifies self.config). The vertex v is fired only once, even if the result leaves v unstable.
—
first_diffs_hilb()
Returns the first differences of the Hilbert function of the homogeneous sandpile ideal.
INPUT:
None
OUTPUT:
list of nonnegative integers
EXAMPLES:
sage: S = sandlib('generic') sage: S.hilbert_function() [1, 5, 11, 15] sage: S.first_diffs_hilb() [1, 4, 6, 4]
—
groebner()
Returns a Groebner basis for the homogeneous sandpile ideal with respect to the standard sandpile ordering (see ring).
INPUT:
None
OUTPUT:
Groebner basis
EXAMPLES:
sage: S = sandlib('generic') sage: S.groebner() x_2-x_0, x_3^2-x_5*x_0, x_5*x_3-x_0^2, x_4^2-x_3*x_1, x_5^2-x_3*x_0, x_1^3-x_4*x_3*x_0, x_4*x_1^2-x_5*x_0^2
—
group_order()
Returns the size of the sandpile group.
INPUT:
None
OUTPUT:
int
EXAMPLES:
sage: G = sandlib('generic') sage: G.group_order() 15
—
hilbert_function()
Returns the Hilbert function of the homogeneous sandpile ideal.
INPUT:
None
OUTPUT:
list of nonnegative integers
EXAMPLES:
sage: S = sandlib('generic') sage: S.hilbert_function() [1, 5, 11, 15]
—
ideal()
The saturated, homogeneous sandpile ideal.
INPUT:
None
OUTPUT:
ideal
EXAMPLES:
sage: S = sandlib('generic') sage: S.ideal() x_2-x_0, x_3^2-x_5*x_0, x_5*x_3-x_0^2, x_4^2-x_3*x_1, x_5^2-x_3*x_0, x_1^3-x_4*x_3*x_0, x_4*x_1^2-x_5*x_0^2
—
identity()
Returns the identity configuration.
INPUT:
None
OUTPUT:
dict (the identity configuration)
EXAMPLES:
sage: G = sandlib('generic') sage: e = G.identity() sage: x = G.stably_add(e, G.max_stable()) sage: x [{1: 2, 2: 2, 3: 1, 4: 1, 5: 1}, {1: 1, 2: 5, 3: 7, 4: 1, 5: 6}] sage: G.config_to_list(x[0]) [2, 2, 1, 1, 1] sage: G.config_to_list(G.max_stable()) [2, 2, 1, 1, 1]
—
in_degree(v=None)
Return the in-degree of a vertex or a list of all in-degrees.
INPUT:
v - vertex name or None
OUTPUT:
integer or list of integers
EXAMPLES:
sage: G = sandlib('generic') sage: G.in_degree(2) 2 sage: G.in_degree() {0: 2, 1: 1, 2: 2, 3: 4, 4: 1, 5: 2}
—
is_recurrent(config=None)
Returns True if config is recurrent, i.e., is an element of the sandpile group.
INPUT:
config (optional) - dict (configuration)
OUTPUT:
boolean
EXAMPLES:
sage: S = sandlib('generic') sage: S.is_recurrent(S.identity()) True sage: c = S.list_to_config([0,0,0,0,0]) sage: S.is_recurrent(c) False
—
is_stable(config=None)
Returns True if config is stable.
INPUT:
config (optional) - dict (configuration)
OUTPUT:
boolean
EXAMPLES:
sage: S = sandlib('generic') sage: S.is_stable(S.max_stable()) True sage: c = S.add(S.max_stable(), S.max_stable()) sage: S.is_stable(c) False
—
is_superstable(config=None)
Returns True if config is superstable, i.e., it does not permit multiset firings.
INPUT:
config (optional) - dict (configuration)
OUTPUT:
boolean
EXAMPLES:
sage: S = sandlib('generic') sage: S.is_superstable(S.identity()) False sage: c = S.subtract(S.max_stable(), S.identity()) sage: S.is_superstable(c) True
—
is_symmetric(c, orbits)
This function checks if
is constant over the vertices in each sublist of orbits.
INPUT:
- c - configuration
- orbit - list of lists of vertices
OUTPUT:
boolean
EXAMPLES:
sage: S = sandlib('kite') sage: S.dict() {0: {}, 1: {0: 1, 2: 1, 3: 1}, 2: {1: 1, 3: 1, 4: 1}, 3: {1: 1, 2: 1, 4: 1}, 4: {2: 1, 3: 1}} sage: c = S.list_to_config([1, 2, 2, 3]) sage: S.is_symmetric(c,[[2,3]]) True
—
laplacian()
Returns the Laplacian matrix of the graph.
INPUT:
None
OUTPUT:
matrix
EXAMPLES:
sage: G = sandlib('generic') sage: G.laplacian() [ 0 0 0 0 0 0] [-1 3 0 -1 -1 0] [-1 0 3 -1 0 -1] [ 0 0 -1 2 0 -1] [ 0 -1 0 -1 2 0] [ 0 0 -1 -1 0 2]
—
linear_system(div)
Returns the complete linear system of a divisor.
INPUT:
div - divisor
OUTPUT:
dict - {num_homog: int, homog:list, num_inhomog:int, inhomog:list}
EXAMPLES:
sage: S = sandlib('generic') sage: D = S.list_to_div([0,0,0,0,0,2]) sage: S.linear_system(D) {'homog': [[1, 0, 0, 0, 0, 0], [-1, 0, 0, 0, 0, 0]], 'inhomog': [[0, 0, -1, -1, 0, -2], [0, 0, 0, 0, 0, -1], [0, 0, 0, 0, 0, 0]], 'num_homog': 2, 'num_inhomog': 3}NOTES:
If
is the Laplacian, an arbitrary
such that
has the form
where
is in inhomg and
is in the integer span of homog in the output of linear_system(D).
WARNING:
This method requires 4ti2. After local installation of 4ti2, set the path_to_zsolve at the beginning of sandpile.sage.
—
list_to_config(L)
Convert a list into a configuration.
INPUT:
L - list of nonnegative integers
OUTPUT:
dict (configuration)
EXAMPLES:
sage: S = sandlib('generic') sage: S.list_to_config([3,6,4,2,4]) {1: 3, 2: 6, 3: 4, 4: 2, 5: 4}NOTES:
The method checks the length of L but not the types of its entries.
—
list_to_div(L)
Convert a list of integers into a divisor.
INPUT:
L - list of integers
OUTPUT:
dict (configuration)
EXAMPLES:
sage: S = sandlib('generic') sage: S.list_to_div([6,5,4,3,2,1]) {0: 6, 1: 5, 2: 4, 3: 3, 4: 2, 5: 1}NOTES:
The method checks the length of L but not the types of its entries.
—
max_stable()
Returns the maximal stable configuration.
INPUT:
None
OUTPUT:
dict (the maximal stable configuration)
EXAMPLES:
sage: G = sandlib('generic') sage: G.max_stable() {1: 2, 2: 2, 3: 1, 4: 1, 5: 1}
—
nonsink_vertices()
The names of the nonsink vertices.
INPUT:
None
OUTPUT:
None
EXAMPLES:
sage: G = sandlib('generic') sage: G.nonsink_vertices() [1, 2, 3, 4, 5]
—
out_degree(v=None)
Return the out-degree of a vertex or a list of all out-degrees.
INPUT:
v (optional) - vertex name
OUTPUT:
integer or list of integers
EXAMPLES:
sage: G = sandlib('generic') sage: G.out_degree(2) 3 sage: G.out_degree() {0: 0, 1: 3, 2: 3, 3: 2, 4: 2, 5: 2}
—
points()
Returns generators for the multiplicative group of zeros of the sandpile ideal.
INPUT:
None
OUTPUT:
list of complex numbers
EXAMPLES:
The sandpile group in this example is cyclic, and hence there is a single generator for the group of solutions.
sage: S = sandlib('generic') sage: S.points() [[e^(4/5*I*pi), 1, e^(2/3*I*pi), e^(-34/15*I*pi), e^(-2/3*I*pi)]]
—
postulation()
Returns the postulation number of the sandpile ideal. This is the largest weight of a superstable configuration of the graph.
INPUT:
None
OUTPUT:
nonnegative integer
EXAMPLES:
sage: S = sandlib('generic') sage: S.postulation() 3
—
r_of_D(D)
Computes r(D) and an effective divisor F such that |D - F| is empty.
INPUT:
D - divisor
OUTPUT:
tuple ((integer r(D), divisor F))
EXAMPLES:
sage: S = sandlib('generic') sage: D = S.list_to_div([0,0,0,0,0,4]) sage: E = S.r_of_D(D) 0 1 sage: E (1, {0: 0, 1: 1, 2: 0, 3: 1, 4: 0, 5: 0}) sage: F = E[1] sage: S.div_to_list(S.subtract(D,F)) [0, -1, 0, -1, 0, 4] sage: S.effective_div(S.subtract(D,F)) [] sage: S.r_of_D(S.list_to_div([0,0,0,0,0,-4])) (-1, {0: 0, 1: 0, 2: 0, 3: 0, 4: 0, 5: -4})
—
recurrent_difference(config1, config2)
Returns a recurrent configuration equivalent to the difference of the two given configurations, config1 - config2.
INPUT:
config1, config2 - dict (configurations)
OUTPUT:
dict (configuration)
EXAMPLES:
sage: S = sandlib('generic') sage: c = S.recurrent_difference(S.max_stable(), S.max_stable()) sage: c {1: 2, 2: 2, 3: 1, 4: 1, 5: 0} sage: c == S.identity() True
—
recurrents(verbose=True)
Returns the list of recurrent configurations as dictionaries if verbose is True, otherwise as lists of integers.
INPUT:
verbose (optional) – boolean
OUTPUT:
list (of recurrent configurations)
EXAMPLES:
sage: S = sandlib('generic') sage: S.recurrents() [{1: 2, 2: 2, 3: 1, 4: 1, 5: 1}, {1: 2, 2: 2, 3: 0, 4: 1, 5: 1}, {1: 0, 2: 2, 3: 1, 4: 1, 5: 0}, {1: 0, 2: 2, 3: 1, 4: 1, 5: 1}, {1: 1, 2: 2, 3: 1, 4: 1, 5: 1}, {1: 1, 2: 2, 3: 0, 4: 1, 5: 1}, {1: 2, 2: 2, 3: 1, 4: 0, 5: 1}, {1: 2, 2: 2, 3: 0, 4: 0, 5: 1}, {1: 2, 2: 2, 3: 1, 4: 0, 5: 0}, {1: 1, 2: 2, 3: 1, 4: 1, 5: 0}, {1: 1, 2: 2, 3: 1, 4: 0, 5: 0}, {1: 1, 2: 2, 3: 1, 4: 0, 5: 1}, {1: 0, 2: 2, 3: 0, 4: 1, 5: 1}, {1: 2, 2: 2, 3: 1, 4: 1, 5: 0}, {1: 1, 2: 2, 3: 0, 4: 0, 5: 1}] sage: S.recurrents(false) [[2, 2, 1, 1, 1], [2, 2, 0, 1, 1], [0, 2, 1, 1, 0], [0, 2, 1, 1, 1], [1, 2, 1, 1, 1], [1, 2, 0, 1, 1], [2, 2, 1, 0, 1], [2, 2, 0, 0, 1], [2, 2, 1, 0, 0], [1, 2, 1, 1, 0], [1, 2, 1, 0, 0], [1, 2, 1, 0, 1], [0, 2, 0, 1, 1], [2, 2, 1, 1, 0], [1, 2, 0, 0, 1]]
—
reduced_laplacian()
Returns the reduced Laplacian matrix of the graph.
INPUT:
None
OUTPUT:
matrix
EXAMPLES:
sage: G = sandlib('generic') sage: G.laplacian() [ 0 0 0 0 0 0] [-1 3 0 -1 -1 0] [-1 0 3 -1 0 -1] [ 0 0 -1 2 0 -1] [ 0 -1 0 -1 2 0] [ 0 0 -1 -1 0 2] sage: G.reduced_laplacian() [ 3 0 -1 -1 0] [ 0 3 -1 0 -1] [ 0 -1 2 0 -1] [-1 0 -1 2 0] [ 0 -1 -1 0 2]NOTES:
This is the Laplacian matrix with the row and column indexed by the sink vertex removed.
—
reset_config(config=None)
Turn config into the zero configuration.
INPUT:
config (optional) - dict
OUTPUT:
None
EXAMPLES:
sage: G = sandlib('generic') sage: G.add(G.max_stable(),G.max_stable()) {1: 4, 2: 4, 3: 2, 4: 2, 5: 2} sage: G.config() {1: 4, 2: 4, 3: 2, 4: 2, 5: 2} sage: G.reset_config() sage: G.config() {1: 0, 2: 0, 3: 0, 4: 0, 5: 0}
—
resolution(verbose=False)
This function computes a minimal free resolution of the homogeneous sandpile ideal. If verbose is True, then all of the mappings are returned. Otherwise, the resolution is summarized.
INPUT:
verbose (optional) - boolean
OUTPUT:
free resolution of the sandpile ideal
EXAMPLES:
sage: S = Sandpile({0: {}, 1: {2: 2}, 2: {0: 4, 1: 1}}, 0) sage: S.resolution() 'R <-- R^2 <-- R^1' sage: S.resolution(verbose=True) [1]: _[1]=x_1^2-x_2^2 _[2]=x_1*x_2^3-x_0^4 [2]: _[1]=x_1*x_2^3*gen(1)-x_0^4*gen(1)-x_1^2*gen(2)+x_2^2*gen(2) [3]: _[1]=0
—
ring()
The ring containing the homogeneous sandpile ideal.
INPUT:
None
OUTPUT:
ring
EXAMPLES:
sage: S = sandlib('generic') sage: S.ring() // characteristic : 0 // number of vars : 6 // block 1 : ordering dp // : names x_5 x_4 x_3 x_2 x_1 x_0 // block 2 : ordering CNOTES:
The indeterminate
corresponds to the
-th vertex as listed my the method vertices. The term-ordering is degrevlex with indeterminates ordered according to their distance from the sink (larger indeterminates are further from the sink).
—
set_config(config)
Sets the current configuration to config.
INPUT:
config - dict
OUTPUT:
None
EXAMPLES:
sage: G = sandlib('generic') sage: G.set_config(G.identity()) sage: G.config() == G.identity() True
—
sink()
Returns the identifier for the sink vertex.
INPUT:
None
OUTPUT: Object (name for the sink vertex)
EXAMPLES:
sage: G = sandlib('generic') sage: G.sink() 0 sage: H = Sandpile(grid(2,2),'sink') sage: H.sink() 'sink' sage: type(H.sink()) <type 'str'>
—
solve()
Computes approximations of the complex affine zeros of the sandpile ideal.
INPUT:
None
OUTPUT:
list of complex numbers
EXAMPLES:
sage: S = Sandpile({0: {}, 1: {2: 2}, 2: {0: 4, 1: 1}}, 0) sage: S.solve() [[0.707107*I - 0.707107, 0.707107 - 0.707107*I], [-0.707107*I - 0.707107, 0.707107*I + 0.707107], [-1*I, -1*I], [I, I], [0.707107*I + 0.707107, -0.707107*I - 0.707107], [0.707107 - 0.707107*I, 0.707107*I - 0.707107], [1, 1], [-1, -1]] sage: len(_) 8 sage: S.group_order() 8NOTES:
The solutions form a multiplicative group isomorphic to the sandpile group. Generators for this group are given exactly by points().
—
stabilize(config=None)
Returns the stabilized configuration and its firing vector.
INPUT:
config (optional) - dict
OUTPUT:
list - [out_config, firing_vector]
EXAMPLES:
sage: S = sandlib('generic') sage: c = S.add(S.max_stable(), S.identity()) sage: S.stabilize(c) [{1: 2, 2: 2, 3: 1, 4: 1, 5: 1}, {1: 1, 2: 5, 3: 7, 4: 1, 5: 6}]The Sandpiles current configuration is modified:
sage: S.config() {1: 2, 2: 2, 3: 1, 4: 1, 5: 1}
—
stabilize_one_step(config=None)
Fire each unstable vertex in config, returning a list [out_config, firing_vector] where out_config is the modified configuration.
INPUT:
config (optional) - dict
OUTPUT:
list of the form [dict, dict]
EXAMPLES:
sage: G = sandlib('generic') sage: c = G.add(G.max_stable(),G.identity()) sage: c {1: 4, 2: 4, 3: 2, 4: 2, 5: 1} sage: G.unstable(c) [1, 2, 3, 4] sage: G.stabilize_one_step(c) [{1: 2, 2: 2, 3: 3, 4: 1, 5: 3}, {1: 1, 2: 1, 3: 1, 4: 1, 5: 0}]
—
stably_add(config1, config2)
Returns the stabilization and corresponding firing vector of the sum of two configurations.
INPUT:
config1, config2 - dict (configurations)
OUTPUT:
list ([stabilized sum, firing_vector])
EXAMPLES:
sage: S = sandlib('generic') sage: S.stably_add(S.max_stable(), S.max_stable()) [{1: 2, 2: 2, 3: 0, 4: 1, 5: 1}, {1: 1, 2: 7, 3: 10, 4: 1, 5: 9}]
—
subtract(c, d)
Returns the difference, c - d.
INPUT:
c, d - dict (configurations or divisors)
OUTPUT:
dict (configuration or divisor)
EXAMPLES:
Subtracting configurations:
sage: S = sandlib('generic') sage: m = S.max_stable() sage: m {1: 2, 2: 2, 3: 1, 4: 1, 5: 1} sage: S.subtract(m, m) {1: 0, 2: 0, 3: 0, 4: 0, 5: 0}Subtracting divisors:
sage: D = S.list_to_div([1,-3,2,0,4,-2]) sage: E = S.list_to_div([2, 3,4,1,1,-2]) sage: S.subtract(D,E) {0: -1, 1: -6, 2: -2, 3: -1, 4: 3, 5: 0}
—
superstables(verbose=True)
Returns the list of superstable configurations as dictionaries if verbose is True, otherwise as lists of integers. The superstables are also known as
-parking functions.
INPUT:
verbose - boolean
OUTPUT:
list (of superstable elements)
EXAMPLES:
sage: S = sandlib('generic') sage: S.superstables() [{1: 0, 2: 0, 3: 0, 4: 0, 5: 0}, {1: 0, 2: 0, 3: 1, 4: 0, 5: 0}, {1: 2, 2: 0, 3: 0, 4: 0, 5: 1}, {1: 2, 2: 0, 3: 0, 4: 0, 5: 0}, {1: 1, 2: 0, 3: 0, 4: 0, 5: 0}, {1: 1, 2: 0, 3: 1, 4: 0, 5: 0}, {1: 0, 2: 0, 3: 0, 4: 1, 5: 0}, {1: 0, 2: 0, 3: 1, 4: 1, 5: 0}, {1: 0, 2: 0, 3: 0, 4: 1, 5: 1}, {1: 1, 2: 0, 3: 0, 4: 0, 5: 1}, {1: 1, 2: 0, 3: 0, 4: 1, 5: 1}, {1: 1, 2: 0, 3: 0, 4: 1, 5: 0}, {1: 2, 2: 0, 3: 1, 4: 0, 5: 0}, {1: 0, 2: 0, 3: 0, 4: 0, 5: 1}, {1: 1, 2: 0, 3: 1, 4: 1, 5: 0}] sage: S.superstables(false) [[0, 0, 0, 0, 0], [0, 0, 1, 0, 0], [2, 0, 0, 0, 1], [2, 0, 0, 0, 0], [1, 0, 0, 0, 0], [1, 0, 1, 0, 0], [0, 0, 0, 1, 0], [0, 0, 1, 1, 0], [0, 0, 0, 1, 1], [1, 0, 0, 0, 1], [1, 0, 0, 1, 1], [1, 0, 0, 1, 0], [2, 0, 1, 0, 0], [0, 0, 0, 0, 1], [1, 0, 1, 1, 0]]
—
support(D)
The input is a dictionary of integers. The output is a list of keys of nonzero values of the dictionary.
INPUT:
D - dict (configuration or divisor)
OUTPUT:
list - support of the configuration or divisor
EXAMPLES:
sage: S = sandlib('generic') sage: c = S.identity() sage: S.config_to_list(c) [2, 2, 1, 1, 0] sage: S.support(c) [1, 2, 3, 4] sage: S.vertices() [0, 1, 2, 3, 4, 5]
—
symmetric_recurrents(orbits)
Returns the list of symmetric recurrent configurations.
INPUT:
orbits - list of lists partitioning the vertices
OUTPUT:
list of recurrent configurations
EXAMPLES:
sage: S = sandlib('kite') sage: S.dict() {0: {}, 1: {0: 1, 2: 1, 3: 1}, 2: {1: 1, 3: 1, 4: 1}, 3: {1: 1, 2: 1, 4: 1}, 4: {2: 1, 3: 1}} sage: S.symmetric_recurrents([[1],[2,3],[4]]) [{1: 2, 2: 2, 3: 2, 4: 1}, {1: 2, 2: 2, 3: 2, 4: 0}] sage: S.recurrents() [{1: 2, 2: 2, 3: 2, 4: 1}, {1: 2, 2: 2, 3: 2, 4: 0}, {1: 2, 2: 1, 3: 2, 4: 0}, {1: 2, 2: 2, 3: 0, 4: 1}, {1: 2, 2: 0, 3: 2, 4: 1}, {1: 2, 2: 2, 3: 1, 4: 0}, {1: 2, 2: 1, 3: 2, 4: 1}, {1: 2, 2: 2, 3: 1, 4: 1}]NOTES:
The user is responsible for ensuring that the list of orbits comes from a group of symmetries of the underlying graph.
—
unsaturated_ideal()
The unsaturated, homogeneous sandpile ideal.
INPUT:
None
OUTPUT:
ideal
EXAMPLES:
sage: S = sandlib('generic') sage: S.unsaturated_ideal() x_1^3-x_4*x_3*x_0, x_2^3-x_5*x_3*x_0, x_3^2-x_5*x_2, x_4^2-x_3*x_1, x_5^2-x_3*x_2 sage: S.ideal() x_2-x_0, x_3^2-x_5*x_0, x_5*x_3-x_0^2, x_4^2-x_3*x_1, x_5^2-x_3*x_0, x_1^3-x_4*x_3*x_0, x_4*x_1^2-x_5*x_0^2
—
unstable(config=None)
The list of unstable vertices in config.
INPUT:
config (optional) - dict
OUTPUT:
list of vertex names
EXAMPLES:
sage: G = sandlib('generic') sage: c = G.add(G.max_stable(),G.identity()) sage: G.unstable(c) [1, 2, 3, 4] sage: G.stabilize(c); sage: G.unstable(c) []
—
version()
Returns the version number of Sage Sandpiles.
INPUT:
None
OUTPUT:
string
EXAMPLES:
sage: S = sandlib('generic') sage: S.version() Sage Sandpiles Version 1.5
—
vertices(boundary_first=False))
Return a list of the vertices.
INPUT:
- boundary_first - Return the boundary vertices first.
EXAMPLE:
sage: P = graphs.PetersenGraph() sage: P.vertices() [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]Note that the output of the vertices() function is always sorted. This is sub-optimal, speedwise, but note the following optimizations:
sage: timeit V = P.vertices() # not tested 100000 loops, best of 3: 8.85 [micro]s per loop sage: timeit V = list(P.vertex_iterator()) # not tested 100000 loops, best of 3: 5.74 [micro]s per loop sage: timeit V = list(P._nxg.adj.iterkeys()) # not tested 100000 loops, best of 3: 3.45 [micro]s per loopIn other words, if you want a fast vertex iterator, call the dictionary directly.
Utility methods¶
The following methods create Sandpiles. (See the examples in the complete descriptions.)
- aztec(n) — The aztec diamond graph.
- sandlib(selector) — A collection of sandpiles.
- grid(m, n) — The
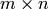 grid graph.
grid graph. - random_graph(num_verts, p, directed, weight_max) — A random graph.
- random_DAG(num_verts, p, weight_max) — A random directed acyclic graph.
- glue_graphs(g, h, glue_g, glue_h) — Glue two sandpiles together.
Complete descriptions of methods.
aztec(n)
The aztec diamond graph.
INPUT:
n - integer
OUTPUT:
dictionary for the aztec diamond graph
EXAMPLES:
sage: aztec(2) {(-3/2, -1/2): {}, (-3/2, 1/2): {}, (-1/2, -3/2): {'sink': 2, (-1/2, -1/2): 1, (1/2, -3/2): 1}, (-1/2, -1/2): {(-3/2, -1/2): 1, (-1/2, -3/2): 1, (-1/2, 1/2): 1, (1/2, -1/2): 1}, (-1/2, 1/2): {(-3/2, 1/2): 1, (-1/2, -1/2): 1, (-1/2, 3/2): 1, (1/2, 1/2): 1}, (-1/2, 3/2): {}, (1/2, -3/2): {}, (1/2, -1/2): {(-1/2, -1/2): 1, (1/2, -3/2): 1, (1/2, 1/2): 1, (3/2, -1/2): 1}, (1/2, 1/2): {(-1/2, 1/2): 1, (1/2, -1/2): 1, (1/2, 3/2): 1, (3/2, 1/2): 1}, (1/2, 3/2): {}, (3/2, -1/2): {}, (3/2, 1/2): {}} sage: Sandpile(aztec(2),'sink').group_order() 4542720NOTES:
This is the aztec diamond graph with a sink vertex added. Boundary vertices have edges to the sink so that each vertex has degree 4.
—
sandlib(selector=None)
Returns the sandpile identified by selector. If no argument is given, a description of the sandpiles in the sandlib is printed.
INPUT:
selector - identifier or None
OUTPUT:
sandpile or description
EXAMPLES:
sage: sandlib() Sandpiles in the sandlib: kite : generic undirected graphs with 5 vertices generic : generic digraph with 6 vertices ci1 : complete intersection, non-DAG but equivalent to a DAG riemann-roch1 : directed graph with postulation 9 and 3 maximal weight superstables riemann-roch2 : directed graph with a superstable not majorized by a maximal superstable gor : Gorenstein but not a complete intersection sage: S = sandlib('gor') sage: S.resolution() 'R <-- R^5 <-- R^5 <-- R^1'
—
grid(m, n)
The mxn grid graph. Each nonsink vertex has degree 4.
INPUT: m, n - positive integers
OUTPUT: dictionary for a sandpile with sink named sink.
EXAMPLE:
sage: grid(3,4) {'sink': {}, (1, 1): {'sink': 2, (1, 2): 1, (2, 1): 1}, (1, 2): {'sink': 1, (1, 1): 1, (1, 3): 1, (2, 2): 1}, (1, 3): {'sink': 1, (1, 2): 1, (1, 4): 1, (2, 3): 1}, (1, 4): {'sink': 2, (1, 3): 1, (2, 4): 1}, (2, 1): {'sink': 1, (1, 1): 1, (2, 2): 1, (3, 1): 1}, (2, 2): {(1, 2): 1, (2, 1): 1, (2, 3): 1, (3, 2): 1}, (2, 3): {(1, 3): 1, (2, 2): 1, (2, 4): 1, (3, 3): 1}, (2, 4): {'sink': 1, (1, 4): 1, (2, 3): 1, (3, 4): 1}, (3, 1): {'sink': 2, (2, 1): 1, (3, 2): 1}, (3, 2): {'sink': 1, (2, 2): 1, (3, 1): 1, (3, 3): 1}, (3, 3): {'sink': 1, (2, 3): 1, (3, 2): 1, (3, 4): 1}, (3, 4): {'sink': 2, (2, 4): 1, (3, 3): 1}} sage: S = Sandpile(grid(3,4),'sink') sage: S.group_order() 4140081
—
random_graph(num_verts, p=1/2, directed=True, weight_max=1)
A random weighted digraph with a directed spanning tree rooted at
. If directed = False, the only difference is that if
is an edge with tail
, head
, and weight
, then
appears also. The result is returned as a Sage digraph.
INPUT:
- num_verts - number of vertices
- p - probability edges occur
- directed - True if directed
- weight_max - integer maximum for random weights
OUTPUT:
random graph
EXAMPLES:
sage: g = random_graph(6,0.2,True,3) sage: S = Sandpile(g,0) sage: S.show(edge_labels = True)
—
random_DAG(num_verts, p=1/2, weight_max=1)
Returns a random directed acyclic graph with num_verts vertices. The method starts with the sink vertex and adds vertices one at a time. Each vertex is connected only to only previously defined vertices, and the probability of each possible connection is given by the argument p. The weight of an edge is a random integer between 1 and weight_max.
INPUT:
- num_verts - positive integer
- p - number between
and
- weight_max – integer greater than
OUTPUT:
directed acyclic graph with sink
EXAMPLES:
sage: S = random_DAG(5, 0.3)
—
glue_graphs(g, h, glue_g, glue_h)
Glue two graphs together.
INPUT:
- g, h - dictionaries for directed multigraphs
- glue_h, glue_g - dictionaries for a vertex
OUTPUT:
dictionary for a directed multigraph
EXAMPLES:
sage: x = {0: {}, 1: {0: 1}, 2: {0: 1, 1: 1}, 3: {0: 1, 1: 1, 2: 1}} sage: y = {0: {}, 1: {0: 2}, 2: {1: 2}, 3: {0: 1, 2: 1}} sage: glue_x = {1: 1, 3: 2} sage: glue_y = {0: 1, 1: 2, 3: 1} sage: z = glue_graphs(x,y,glue_x,glue_y) sage: z {0: {}, 'x0': {0: 1, 'x1': 1, 'x3': 2, 'y1': 2, 'y3': 1}, 'x1': {'x0': 1}, 'x2': {'x0': 1, 'x1': 1}, 'x3': {'x0': 1, 'x1': 1, 'x2': 1}, 'y1': {0: 2}, 'y2': {'y1': 2}, 'y3': {0: 1, 'y2': 1}} sage: S = Sandpile(z,0) sage: S.first_diffs_hilb() [1, 6, 17, 31, 41, 41, 31, 17, 6, 1] sage: S.resolution() 'R <-- R^7 <-- R^21 <-- R^35 <-- R^35 <-- R^21 <-- R^7 <-- R^1'NOTES:
This method makes a dictionary for a graph by combining those for g and h. The sink of g is replaced by a vertex that is connected to the vertices of g as specified by glue_g the vertices of h as specified in glue_h. The sink of the glued graph is
.
Both glue_g and glue_h are dictionaries with entries of the form v:w where v is the vertex to be connected to and w is the weight of the connecting edge.
Help¶
Documentation for each method is available through the Sage online help system:
sage: Sandpile.fire_vertex?
Namespace: Interactive
File: /home/davidp/.sage/temp/xyzzy/7883/_home_davidp_math_sandpile_sage_sage_sandpile1_4_sandpile_sage_47.py
Definition: Sandpile.fire_vertex(self, v, config=None)
Docstring:
Fire (topple) a given vertex of a configuration.
INPUT:
- ``v`` - vertex name
- ``config`` - dict
OUTPUT:
dict (configuration)
EXAMPLES::
sage: G = sandlib('generic')
sage: c = G.add(G.max_stable(),G.identity())
sage: G.unstable(c)
[1, 2, 3, 4]
sage: c
{1: 4, 2: 4, 3: 2, 4: 2, 5: 1}
sage: G.fire_vertex(1,c)
NOTES:
This method fires vertex ``v`` in ``config`` provided ``v`` is a
nonsink, unstable vertex. Returns the result (and modifies
``self.config``). The vertex ``v`` is fired only once, even if the
result leaves ``v`` unstable.
Note
An alternative to Sandpile.fire_vertex? in the preceding code example would be S.fire_vertex?, if S is any sandpile.
General Sage documentation can be found at http://sagemath.org/doc/.
Contact¶
Please contact davidp@reed.edu with questions, bug reports, and suggestions for additional features and other improvements.
| [BN] | Matthew Baker, Serguei Norine, Riemann-Roch and Abel-Jacobi Theory on a Finite Graph, Advances in Mathematics 215 (2007), 766–788. |
| [BTW] | Per Bak, Chao Tang and Kurt Wiesenfeld (1987). Self-organized criticality: an explanation of 1/ƒ noise, Physical Review Letters 60: 381–384 Wikipedia article. |
| [H] | Holroyd, Levine, Meszaros, Peres, Propp, Wilson, Chip-Firing and Rotor-Routing on Directed Graphs. The final version of this paper appears in In and out of Equilibrium II, Eds. V. Sidoravicius, M. E. Vares, in the Series Progress in Probability, Birkhauser (2008). |
| [PP] | David Perkinson and Jacob Perlman, The algebraic geometry of sandpile groups, preprint (2009). |